Практикум "Математические модели в экономике": семинары и домашние задания, страница 6

Используя результат задачи 25 (а), получаем:

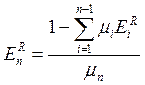
Задача 31

E₁=2, E₁₁=-2.5. Поскольку функция квазилинейная относительно второго параметра, то x₂ от R не зависит, поэтому E₂=0. Далее решаем те же уравнения, что в предыдущей задачи, получаем ответ: E₁₂=0.5, E₂₁=1.5, E₂₂=-1.5

μ₁*2=1 à μ₁=0.5

Задача 32

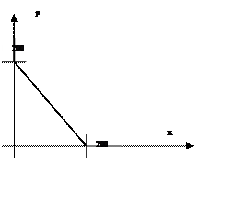 x(p)=max{200-p;0}

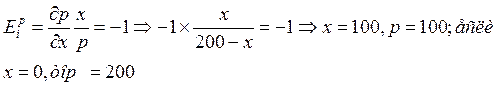
Задача 33

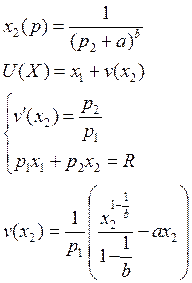
Пусть p₁=1

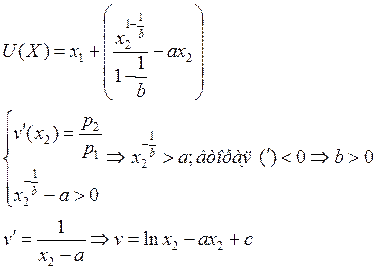
Задача 34

Относительные цены – цены на i-ый товар по отношению к общему уровню цен:

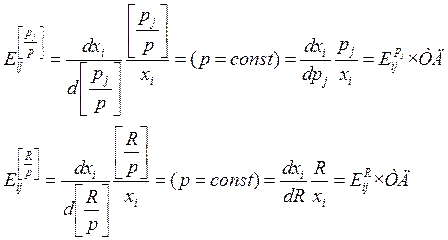
Задача 35

X(p, αR)=αX(p,R)

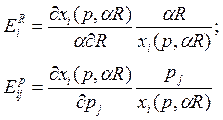
Задача 36

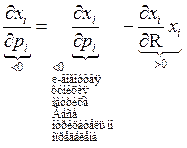
Задача 37

Товар Гиффена: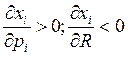

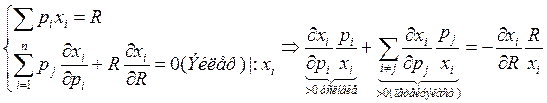ЧТД

Обратно: 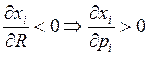НЕ ВЕРНО!

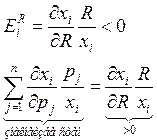
Задача 38

Малоценный товар: 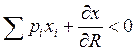Берем производную по R:

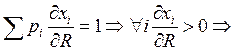все товары не могут быть малоценными.

Задача 39

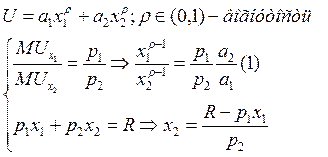Подставляем x₂ в (1). Аккуратно преобразуем и получаем:

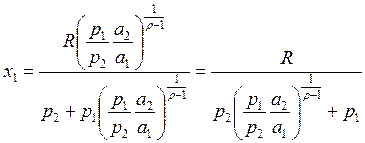 и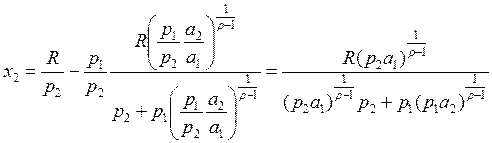

Очевидно, что E_x1,2^R равны единице>0

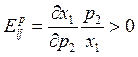
Достаточно посчитать  для определения знака. После преобразования внимательно смотрим на дробь. На знак влияет 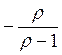. А эта дробь положительна, поскольку 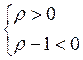ЧТД

Задача 40

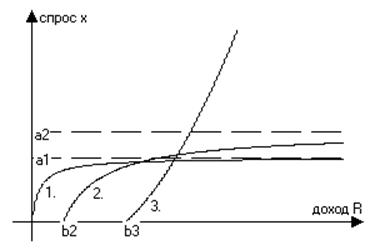
1.  Товары первой необходимости. Функция спроса на эти товары имеет вид

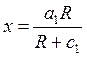, где  

Она отражает тот факт, что рост спроса на товары, удовлетворяющие насущные потребности, постепенно замедляется (так, что 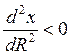). И имеет предел , при  (т.е. кривая асимптотически приближается к линии).

2.  Предметы второй необходимости или товары, эластичность которых близка к единице. Функция спроса:

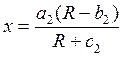, при  и  , , .

Эта функция так же имеет предел , но более высокого уровня чем . Спрос на эту группу товаров появляется, только если уровень дохода превысил уровень

3.  Предметы роскоши, спрос на эту группу товары выражается следующей формулой.

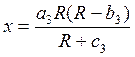, при  и , ,

Предел этой функции равен бесконечности, спрос возникает только после того, как доход превысит

Однако стоит понимать, что функции Торнквиста не всегда объективно отражают ситуацию, они описывают только монотонное изменение спроса, в то время как функция спроса может иметь S-образную форму, может иметь точки максимума и точки перегиба.

Задача 41

b=kp₁ и p₂=1

x₁=(aR)/(R+b)

U=x₁^ax₂^(k-a)(x₁+k-a)^(-k)

Выразим x₂ через x₁

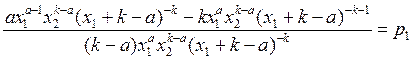После некоторых ОЧЕВИДНЫХ J преобразований придем:

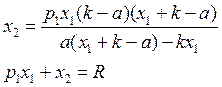Подставим x₂ в бюджетное ограничение, получим после сокращений: x₁=(aR)/(R+b). Что и требовалось показать.

Задача 42

1500 км. R=10000, p₁=10, p₂=5, x₁ – км в купе, x₂ – км в плацкарте.

а)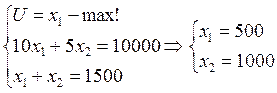

б)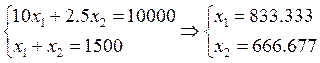

ΔX=333.333

Δp=2.5

ΔX/Δp>0àплацкарт – это товар Гиффена (снижение цены à снижение спроса)

Задача 43

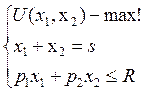
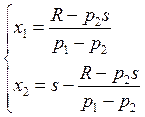
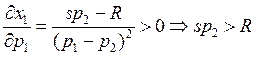А у нас меньше, поэтому купе не может быть товаром Гиффена.

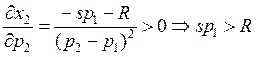 - товар Гиффена всегда! Если бы был меньше R, то индивид бы не поехал в плацкарте.

Задача 44

U(X,S)=X-2√X+S

P_x=0.5

R=20

0.5X+S≤20

ВИД: Поэтому решения – граничные.

(40;0) (0;20); При этом U1=27.35 и U2=20. Поэтому оптимальное решение – (40;0)

Задача 45

а) px=ωL(1-t)

б) (1+t)px=ωL à px=ωL/(1+t`) à 1/(1+t`)=(1-t) – постоянная предельная ставка.

в) T=tR à для государства – да, но ставка, не должна превышать разумных пределов, потому что налог платится с ДОХОДА населения.

Задача 46

а) U(X)=x₁+aln{x₂}

p₁x₁+p₂x₂≤R

x₂=p₁/p₂*a

x₁=R/p₁-a

Если вводится налог на первый товар:

(1+t₁)p₁x₁+p₂x₂≤R

x₂=(1+t)p₁/p₂*a (потребление второго возрастет)

x₁=R/((1+t)p₁)-a (потребление первого снизится)

Если вводится налог на второй товар:

x₂=(1+t)p₁/(1+t)p₂*a (потребление второго снизится)

x₁=R/((1+t)p₁)-a (потребление первого не изменится)

б) U(X)=a₁ln{x₁}+a₂ln{x₂}

p₁x₁+p₂x₂≤R

x₂=a₂/a₁*p₁/p₂*x₁

x₁=a₁R/p₁ при условии, что a₁+a₂=1

Тогда x₂=a₂R/P₂

Если вводится налог на первый товар:

x₁=a₁R/[a₁(1+t)p₁+a₂p₁] (потребление первого снизится) (потребление второго, очевидно, не изменится)

Если вводится налог на первый товар, аналогично, потребление второго снизится, но так как теперь потребление первого тоже зависит от цены второго (обратная зависимость), то оно тоже снизится.

Задача 47

В Аткинсоне, Стиглице не было. Каждую страничку просмотрел! J

U(x)=a₁x₁+a₂√x₂ à max

а) 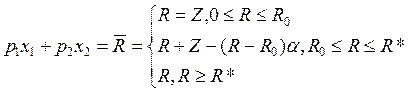 (снижение от заработка, превышающего  величину R₀)

б)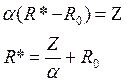

в) Откроем exel J и будем задавать различные параметры для a₁ и a₂ и α от 0 до 1.

Видим, график изменения R и R* имеет такую тенденцию:

Задача 48

Для леонтьевского типа: x₁=(a/b)*x₂ Подставляя, вместо соответствующих значения функций из задач 46 и 47 найдем новые решения.