Экономика и менеджмент \ Математические модели экономики

Практикум "Математические модели в экономике": семинары и домашние задания, страница 3

Решение, которое оптимально по одной из частичных целевых функций является субоптимальным.

В общем случае субоптимальные множества не совпадают, поэтому необходимо выбрать такое множество, которое удовлетворяет всем частичным целевым функциям.

Свойства оценок: [Гранберг]

Критерий – оптимальность по Парето.

оптимально по Парето, если не существует F(x) (допустимого вектора) такого, что и

Задача 1.1.1

Выпускается один вид продукции, при производстве которой затрачивается два вида ресурсов (их количества нельзя выразить в одной единице измерения, например численность занятых и объем капиталовложений). Задана технология производства:

Способ

Затраты ресурсов

Выпуск

1

2

I

2

1

1

II

1

3

2

Требуется выпустить не менее 8 единиц продукции при минимуме затрат как первого, так и второго видов. При этом интенсивность использования каждого из способов должна быть не менее единицы.

РЕШЕНИЕ:

x1 – интенсивность использования первого способа, x2 – интенсивность использования второго способа.

Тогда задача записывается следующим образом:

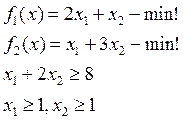
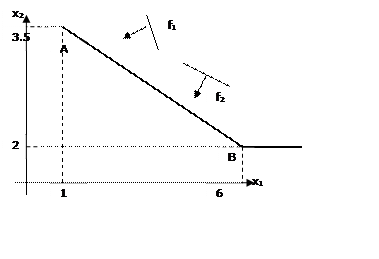
(т)A = (1;3,5) f1(A)=5,5; f2(A)=11,5

(т)B = (6;1) f1(B)=13; f2(B)=9

1) Скаляризация векторного критерия.

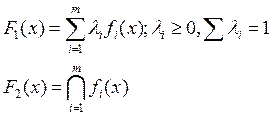
2) Условная субоптимизация.

f1(x)-min!

F*(x)≥Q*

ЭКВИВАЛЕНТНО:

f1(x)-min!              f2(x)-min!

f2(x)≤+∆2  ИЛИ f1(x)≤+∆1

Пусть, например, , тогда F1(x)=0.8(2x1+x2)+0.2(x1+3x2) – min!

f1=2x1+x2 - min!

x1+3x2≤10(9,11.5)

x1+2x2≥8

C=(4;2)

f1(C)=10

f2(C)=10

Пусть теперь затраты на ресурс 2 по способу II уменьшились на единицу:

Способ

Затраты ресурсов

Выпуск

1

2

I

2

1

1

II

1

2

2

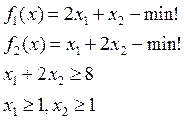
(т)A = (1;3,5) f1(A)=5,5; f2(A)=8

(т)B = (6;1) f1(B)=13; f2(B)=8

Следовательно, точка A оптимальная и для f1 и для f2

1.1.2. Многокритериальная оптимизация

Задача 1.1.2

Пусть для выпуска продукта используется два ресурса. Этот продукт выпускается на двух предприятиях: на предприятии 1 одним способом, на предприятии 2 — двумя

Затраты на ед. продукта

Предприятие 1

Предприятие 2

1

2

Ресурс 1

1

2

3

Ресурс 2

3

2

1,5

а)        Общие для обоих предприятий лимиты ресурсов составляют 12 и 20 единиц. Показать множество эффективных планов распределения выпуска продукции между этими предприятиями.

б)        Пусть лимиты ресурсов закреплены за каждым предприятием:

Затраты на ед. продукции

Предприятие 1

Предприятие 2

Ресурс 1

6

6

Ресурс 2

8

12

Какие точки множества эффективных решений будут устраивать обоих участников?

РЕШЕНИЕ:

а)

x1+x2+x3 – max!

x1+2x2+3x3≤12      |*y1

3x1+2x2+1.5x3≤20 |*y2

Двойственная задача:

g(y)=12y1+20y2-min!

y1+3y2≥1

2y1+2y2≥1

3y1+1.5y2≥1

Проверяем вершины выделенной области (решаем совместно два уравнения и подставляем в третье)

Из 1) и 2) y1=y2=1/4. При этом g(y)=8. А из решения 2) и 3) получаем y1=1/6, y2=1/3. При этом g(y)=8.67.

Таким образом, y1=y2=1/4.

Соответственно, x3=0 и получаем:

x1+x2 – max!

x1+2x2≤12

3x1+2x2≤20

Откуда, x1=x2=4; x3=0

Ищем субоптимальные решения:

I. x1 – max!

x1≤12

3x1≤20 ] x1=62/3

II. x2 – max!

2x2≤12

2x2≤20 ] x2=6

б)

x1 – max!

x1≤6 (*)

3 x1≤8 ] x1=2/3

x2 – max!

2x2≤6

2x2≤12 (*)[5] ] x2=3

Первое предприятие

Оптимально

первый ресурс 1*4 = 6 – 2 (есть 6, можно продавать 2)

второй ресурс 3*4=8 + 4 (покупать 4 единицы второго ресурса)

Второе предприятие

2*4=6+2

2*4=12-4

Следовательно, 2p1=4p2 или p1/p2=2

1.1.3. Взаимные задачи

Общая постановка:

f(x) – max!

k(x)≤b

Предполагаем, что дефицитный ресурс труд, поэтому:

f(x) – max!

q(x)≤Q     (1)

Q – запас труда в системе, q(x) – функция затрат труда.

Рассмотрим множество- множество векторов, которые удовлетворяют (1)

Взаимная задача:

G – граница f(x) – желаемый уровень f(x)

f(x)≥G     (2)

q(x) – min!

Скачать файл