Практикум "Математические модели в экономике": семинары и домашние задания, страница 2

Способ	Себестоимость	Кап вложения	Выпуск
I	2	4	1
II	6 (3)	4 (2)	2 (1) (на единицу выпуска)
III	4	4	1

N=4 (спрос)

K=10 (ограничение на капитал)

РЕШЕНИЕ:

Последний вариант, очевидно, хуже остальных. Сравним два первых.

f(x)=2x₁+6x₂ – min!

4x₁+4x₂≤10

x₁+2x₂≥4

Проверяем вершины в заштрихованном треугольнике. Функция достигает минимума при x₁=1 и x₂=³/₂. Функция достигает при этом значения 11.

Решаем двойственную задачу: (при этом, очевидно, что двойственные переменные – это % и цена)

4x₁+4x₂≤10 |*E

x₁+2x₂≥4     |*V

g(x)=-10E+4V - max!

-4E+V≤2

2E-V≤-3

Ответ: x₁=1 x₂=³/₂ f(x)=11; E=¹/₂ V=4 g(x)=9

Задача 1.0.2

Способ	Себестоимость	Кап вложения	Выпуск
I	4	2	1
II	4 (2)	6 (3)	2 (1) (на единицу выпуска)
III	4	4	1

N=4 (спрос)

K=12 (ограничение на капитал)

РЕШЕНИЕ:

Последний вариант, очевидно, хуже остальных. Сравним два первых.

f(x)= 4x₁+4x₂ – min!

2x₁+6x₂≤12

x₁+2x₂≥4

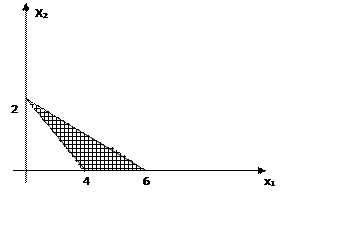
Проверяем вершины в заштрихованном треугольнике. Функция достигает минимума при x₁=0 и x₂=2. Функция достигает при этом значения 8.

Решаем двойственную задачу: (при этом, очевидно, что двойственные переменные – это % и цена)

2x₁+6x₂≤12 |*E

x₁+2x₂≥4     |*V

g(x)=-10E+4V - max!

-2E+V≤4

3E-V≤-2

Ответ: x₁=0 x₂=2 f(x)=8; E=0 V=2 g(x)=8

Этапы экономико-математического моделирования:

1.  Постановка экономической проблемы: формировка вопросов на которые необходимо ответить.

2.  Построение математической модели: формализация 1. Представление модели в виде конкретной экономической зависимости.

3.  Математический анализ модели. Определение существования решений, их устойчивость.

4.  Подготовка численной информации.

5.  Численное решение.

6.  Анализ численных результатов и их применение.

Задача 1.0.3

Проблема соотношения потребления и накопления в национальной экономике (модель потребления и накопления).

РЕШЕНИЕ:

1.

Потребление и накопление:

НД=ФП+ФН

СОП=ФВ+НД[1]

ФН_t∆ОПФ_t+1∆СОП

Допущения:

1)  i=1 (инвестиционного лага нет): ФН_t=∆ОПФ_t+1

2)  Не учитываем НЗП и НЗС[2]

3)  Не учитываем, что величина продукта зависит от трудовых и иных ресурсов.

Критерий: максимизация интегрального фонда потребления[3]

2.

X – величина совокупного общественного продукта.

∆X – прирост продукта в следующий период времени.

Y – национальный доход.

ФВ – фонд возмещения.

ФН – фонд накопления.

ФП – фонд потребления.

1)  X=ФВ+Y

2)  Н=ФН+ФП

3)  ∆X=f(ФН)

a – материалоемкость СОП: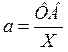

k – капиталоотдача (норма накопления):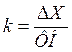

 - норма потребления:

-норма совокупного общественного продукта: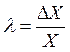

Итак, X=ФВ+Y=ФВ+ФП+ФН=aX+ ФП/=aX+Y+∆X/k

Из 1) следует, X=aX+Y ] X=[1/(1-a)]*Y                 

Из 2) следует, Y=X/k+Y ] Y=[1/(1-)]*X/k                       =(1-a)(1-)k

a,, k постоянны во времени, следовательно, если обозначить
ФП(t) – в момент времени t
Y₀ – НД в начальный момент, тогда:

ФП(t)= Y₀(1+)^t

Пусть  - коэффициент дисконтирования, то есть (1+) показывает, во сколько раз потребление в году t предпочтительнее, чем потребление в году (t+1).

[ ФП(t)/(1+)^t – ФП(t) ] – фонд потребления в году t, приведенный к периоду «0»

Интегральный ФП =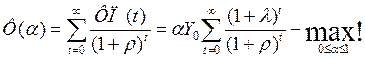

3.

 - max!

 - так как для того, чтобы максимум существовал, ряд должен сходиться (бесконечно убывающая геометрическая прогрессия)

,

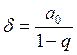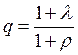
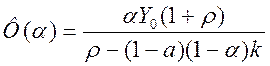
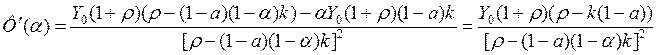
Выводы:

1) Норма потребления может быть любой, поэтому надо проводить корректировку модели:

Пусть k=k₀ (капиталоотдача (норма накопления) пропорциональна норме потребления)

Тогда,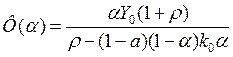

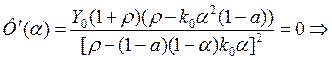
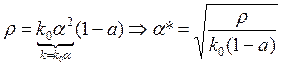
Вспомним условие сходимости ряда (), следовательно,           / Но так как коэффициент материалоемкости меньше единицы ()

Можно усложнить модель - учитывать амортизацию, инвестиционный лаг и чистый экспорт:

X_t=aX_t+[∆X/k](1+)+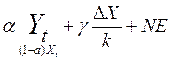[4]

1.1. Целевые установки экономического развития

1.1.1. Многоцелевая (векторная) оптимизация

F(x)=[f₁(x),…,f_m(x)], где f₁ – частичная целевая функция.