Рассмотрим множество
-
множество векторов, которые удовлетворяют (2)
Задача: выявить общие условия для этих задач и найти решение.
Итак, задача:
A. f(x) – max!
(то есть, в этом случае ресурсы зафиксированы
и мы двигаем кривую безразличия)
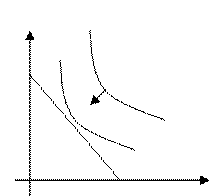
B. g(x) – min!
( в этом случае, напротив, мы изменяем
количество используемых ресурсов для достижения нужной кривой безразличия)
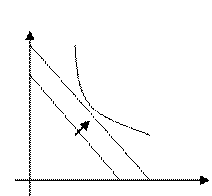
Теорема взаимности.
Если для каждого оптимального x* из задачи A выполнено условие q(x*)=Q, а в задаче B задано, что G=f(x*)? Тогда решения задач A и B совпадают.
Задача 1.1.3
Имеется три продукта, потребляемы в пропорции 50, 30, 20%. Единственным ограниченным ресурсом является труд, удельные затраты которого на производство различных видов продукции составляют соответственно 1; 2; 4,5 единиц. В прямой задаче требуется максимизировать общий фонд потребления при заданном лимите труда в 100 ед.
Если обозначить через x1, x2, x3 объемы производства соответственно первого, второго и третьего продуктов, а через z – общий фонд потребления, то прямая задача будет выглядеть следующим образом.
Найти неотрицательные величины x1, x2, x3, z из условий:
z – max!
x1≥0.5z
x2≥0.3z
x3≥0.2z
x1+2x2+4.5x3≤100 (ограничение по труду)
РЕШЕНИЕ:
Очевидно,
z=50 x1=25, x2=15, x3=10.
Строим двойственную задачу:
z – max!
x1≥0.5z |*v1
x2≥0.3z |*v2
x3≥0.2z |*v3
x1+2x2+4.5x3≤100 |*w
100w – min!
-v1+w=0
-v2+2w=0
-v3+4.5w=0
0.5v1+0.3v2+0.2v3=1
Откуда, v1=0,5, v2=1, v3=2.25, w=0.5
Для взаимной задачи:
q=x1+2x2+4.5x3 – min!
x1≥0.5z |*v1
x2≥0.3z |*v2
x3≥0.2z |*v3
z≥d |*w
q=2z=100=2dàd=50
В прямой задаче, если d>50, то снижается уровень полезности целевой функции q(x)/ И наоборот.
Двойственная задача:
wd – max!
v1=1
v2=2
v3=4.5
-1.5v1-1.3v2-0.2v3+w=0àw=2
Задача 1.1.4
Имеется два продукта. Один из них потребляется домашними хозяйствами. xij – объем i-го продукта, которое использует в производстве j-ое домашнее хозяйство, y- объем потребления.
Найти все параметры системы:
y – max!
x11x21 - y≥10 |*v1
x12x22≥5 |*v2
x11+x12≤10 |*w1
x21+x22≤8 |*w2
xij≥0
РЕШЕНИЕ:
Записываем Лагранжиан:
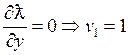
Аналогично, дифференцируем по каждой переменной и придем к системе:
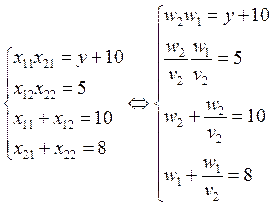Откуда получаем:
Ответ: v2=3, w2=7.5, w1=6, v1=1, x21=6, x11=7.5, x22=2, x21=2.5, y=35
1.2. Модели частичного равновесия (принцип рациональности в поведении отдельных хозяйственных субъектов)
1.2.1. Моделирование сферы потребления
1.2.1.1. Целевая функция потребления
Основные соотношения, которые понадобятся в этой теме:
u(x) – max!
px≤ R |*λ – показывает как изменится целевая функция, при изменении правой части ограничений (иначе говоря – предельная полезность денег)
,
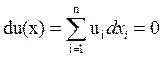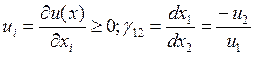
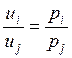! Если все 5 аксиом (смотри лекции)
выполнены, то целевая функция имеет следующий вид:
1)
2) Линейная функция:
3) Функции Леонтьева (блага комплементарны):
4) Если не выполнена пятая аксиома, то функция, очевидно, имеет вид:
x12+x2 Решение на осях!
5) Квазилинейная:
Линейна по одному параметру, например, x1+lgx2
1.2.1.2. Классическая модель потребителя
Задача 2[6]
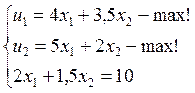
а) Нужно решить задачу для каждого в отдельности:
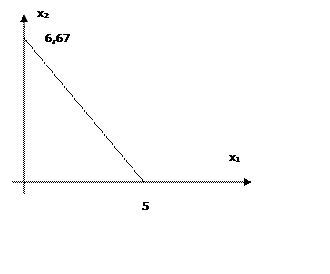
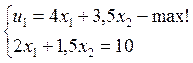
В силу вида кривой полезности, решение будет угловым, и u1=x2=6.67; u2=x1=5
б) В общем виде – 4/p1<3.5/p2 (только второй товар) и 5/p1<2/p2 (только первый товар), откуда наборы сохранятся, если 1.14<p1/p2<2.5
Задача 3[7]
U(x1,x2)=min{x1,x22}; U(x*1,x*2)=9
а) p1=2; R/2=p1=2àR=4; p2=2
Предельная полезность денег = λ
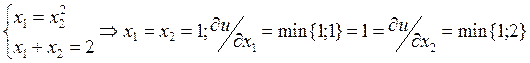
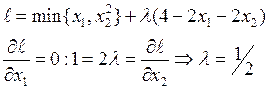
б) R=4,4, но поскольку доля в доходе на расход на оба блага одинакова, то полезность индивида не изменится.
Задача 4
U=min(2x1+x2;x1+2x2); x*1=x*2=4; P1/p2 и R - ?
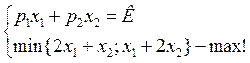u`x1 =min{2;1}=1= u`x2=min{1;2}àp1=p2àR=8p1
Задача 5
Рассмотрим функцию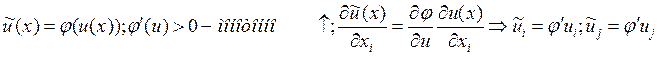 
Тогда, а)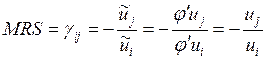 
ЧТД; б) функция спроса: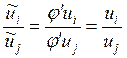 
Задача 6
а) u=x1αx21-α; p1=2; p2=3; x1=10, x2=5
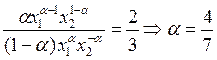
б) Нужно приравнять отношение цен MRS. Если параметры во всех точках не меняются, то функция может быть функцией полезности. В данном случае, во второй таблице в первом случае, α1=α2, но во втором α1=6/5α2 поэтому, это не функция благосостояния.
Задача 7
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.