Задачи
1.График функции распределения вероятностей изображен на рисунке. Найдите связь между а и b.
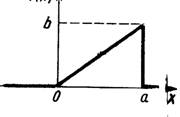
2.Плотность вероятности задана законом
![]()
Найдите а.
3.Найдите математическое ожидание и дисперсию случайной величины, представленной графиком на рисунке.
4.Нормальный закон распределения задан в форме уравнения
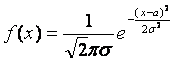 ,
,
причем математическое ожидание равно нулю (а = 0). Какова вероятность того, что случайная величина имеет значения х< а? х>а?
5.В нормальном законе распределения: а = 2; а = 4. Чему равно х, если вероятность того, что случайная величина принимает значения меньше х, равна 3/4?
7. ЛИТЕРАТУРА
1. Конспект лекций.
2. Морозов Ю.В. Основы высшей математики и статистики: Учебник. –М.: Медицина, 1998.–232с.
3. Лобоцкая Н.Л. Основы высшей математики: Изд.2-е, перераб. и доп.– Мн.: Вышэйш. школа, 1978.–480с.
Доцент кафедры медицинской и биологической физики Краморева Л.И.
________________________
(подпись)
________________________
(дата)
Министерство здравоохранения республики Беларусь
Учреждение образования
«Гомельский государственный медицинский университет»
Кафедра медицинской и биологической физики
Обсуждено на заседании кафедры медицинской и биологической физики
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
Для проведения занятия преподавателем со студентами
1 курса лечебного, медико-диагностического, медико-профилактического факультетов по
Тема: Определение соответствия вариационного распределения измеренной величины нормальному закону распределения
Время 135мин
1. УЧЕБНЫЕ И ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ, МОТИВАЦИЯ ДЛЯ УСВОЕНИЯ ТЕМЫ, ТРЕБОВАНИЯ К ИСХОДНОМУ УРОВНЮ ЗНАНИЙ
Методическая разработка предназначена для студентов с целью изучения методов современного математического аппарата как средства решения задач физического, химического, биологического и иного характера, встречающихся как в процессе изучения профильных дисциплин, так и в дальнейшей профессиональной деятельности. Материал пособия может быть использован студентами медицинских факультетов и вузов при изучении раздела «Математическая обработка медико-биологической информации».
Исходный уровень знаний должен включать в себя:
1. Распределение дискретных и непрерывных случайных величин и их характеристики.
2. Нормальный закон распределения.
3. Генеральная совокупность и выборка.
4. Гистограмма.
5. Оценка параметров нормального распределения по опытным данным.
6. Доверительные интервалы для средних.
7. Оценка истинного значения измеряемой величины.
8. Применение распределения Стьюдента для определения доверительных интервалов.
9. Обработка результатов непосредственных и косвенных измерений.
В результате проведения занятия студент должен:
1) Знать основы выборочного метода, позволяющего выяснить закон распределения случайной величины, а также произвести оценку основных числовых характеристик случайной величины.
2) Уметь, используя методы математической статистики, определить закон распределения измеренных случайных величин, заменив безинтервальный ряд на вариационный ряд, а также определить соответствие вариационного распределения измеренной величины нормальному закону распределения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.