Определение соответствия вариационного распределения измеренной величины нормальному закону распределения, страница 13

 Примечание.Значения вероятности даны числами после   запятой.

Тема

Математическая статистика

Относительная частота события
P^*(A)=m/n

где  п — число   независимых   испытаний,   в   которых   случайное событие А происходит m раз.

Вероятность случайного события

P(A)=lim(m/n)  (при n→∞)

Вероятность появления одного (безразлично какого) из нескольких несовместных событий (теорема сложения вероятностей). Для двух событий

P(  А или В) = Р(А) + Р(В).

Вероятность совместного появления независимых событий (теорема умножения вероятностей)

P(А и В) = Р(А)Р(В).

Р(АиВ)=Р(В/А)Р(А)

Для двух событий вероятность того, что событие А произойдет L раз при п испы-таниях (биномиальное распределение)

P_in=n(n-L)•••(n_-L+1)P^L(L-P)^n-L ⁄ L!,

где Р — вероятность наступления события А.

Распределением дискретной случайной величины называют сово-

купность ее значений: х₁, х₂, ... и соответствующих вероятностей:

p(x₁)=p₁, p(x₂)=p₂ ….

Условие нормировки для дискретной случайной величины, имею­щей п значений,

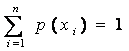
Среднее значение дискретной случайной величины

‹X›=(m_{1 1}+m₂x₂+…+m_nx_n)/n=x₁m₁/n+..+x_nm_n/n

где т_i, — число дискретных случайных величин, имеющих значение  x_i.

Математическое ожидание дискретной случайной величины

M(X)= x₁p₁ +..+x_np_n

Дисперсия дискретной случайной величины

D(X) = M{[X-M(X)]²},

D(X) = M(X²)-[M(X)]²,

Среднее квадратическое отклонение

S(X)=(D(X))^1/2

Вероятность того, что непрерывная случайная величина прини­мает какое-либо значение в интервале (а, b)

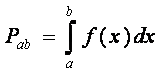
где f(x) — плотность  вероятности   (функция  распределения  вероятностей) .

Условие нормировки для непрерывной случайной величины

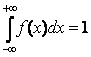
Функция распределения случайной величины

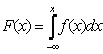
Математическое ожидание непрерывной случайной величины

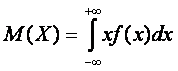
Дисперсия непрерывной случайной величины

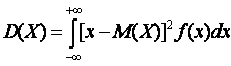
Нормальный закон распределения (закон Гаусса)
где а —  математическое ожидание случайной  величины,   σ - среднее квадратическое отклонение. График закона распределе­ния представлен на рис.

Функция распределения по нормальному закону