Определение соответствия вариационного распределения измеренной величины нормальному закону распределения, страница 14

F(x)=Ф((x-a)/σ)

Значения функции Ф даны в табл.

Плотность вероятности для  проекции    скорости  молекул  газа на ось Ох

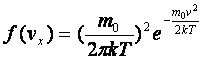
где т_о — масса молекулы, Т — термодинамическая температура газа, k — постоянная Больцмана.

Плотность   вероятности   для   модуля   скорости   молекул    газа (распределение Максвелла по скоростям)

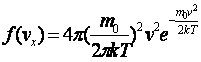
Средняя, средняя квадратичная и навероятнейшая скорости молекул

где R — молярная газовая постоянная, М — молярная масса Плотность вероятности нахождения молекулы газа в однородном гравитационном поле (пример распределения Больцмана)

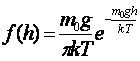
Давление газа  (воздуха), находящегося в однородном гравита­ционном поле, на высоте h (барометрическая формула)

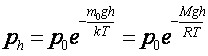
где р_h— давление на высоте h=0

Концентрация молекул газа (воздуха), находящегося в однород­ном гравитационном поле, на высоте h

где n_о — концентрация молекул газа на  высоте h = О

Интервальная оценка генеральной средней (среднее значение ге­неральной совокуп-ности)

‹ x_в› - ε< μ < ‹ x_в› + ε,

где ‹ x_в›   — выборочная средняя   Эти неравенства выполняются с доверительной вероятностью Р   Положительное число ε харак­теризует  точность  оценки   и   называется  доверительным  интер­валом

 При большой выборке (n>30)

τ=(εn^1/2)/σ

где σ - генеральное среднее квадратическое отклонение  Обычно в  расчетах берется  выборочное  среднее  квадратическое  откло­нение

Связь между τ и P  Ф(τ)=(1+P)/2

Интервальная  оценка  генеральной средней  при  малой  выборке

n≤30

ε=ts/n^1/2

Здесь s²=nσ_b²/(n-1)—    исправленная    выборочная    дисперсия,

где σ_b² — выборочная дисперсия  Параметр t (коэффициент Стьюдента) для заданных п и Р находят по табл.

Определить соответствие вариационного распределения измеренной величины нормальному закону распределения

7.  Произвести измерения N величин и записать результаты измерений в протокол.

8.   По результатам измерений построить вариационный ряд.

2.1.- в измеренных величинах найти величину ( х_min) с наименьшим значением и величину (х_max) с  наибольшим значением.

2.2.-определить размах вариации R , представляющий собой  разность между максимальной и        минимальной вариантами совокупности ( R = x_max- x_min).

2.3.-по числу элементов совокупности  N определим число классов К на которые следует разбить совокупность измеренных величин. При N≤100 К определим по формуле

 K= 1+3,32 lg N, при N›100 К определим по формуле  K= 5 lg N .

2.4.-определить величину классового интервала λ , как частное от деления размаха вариации  R на число классов К ,            λ =R/К = (x_max- x_min)/ К.  

Если окажется , что λ=1, собранный материал распределяется в безынтервальный вариационный ряд; если λ≠1, исходные данные необходимо распределить в интервальный ряд.   При этом точность величины классового интервала должна соответствовать точности принятой при измерении величин.

2.5.- определить ширину классов входящих в интервальный вариационный ряд в которых расположатся все измеренные величины от x_max  до  x_min.