Если есть нулевые чисто мнимые корни, то такое движение по Ляпунову называют критическим.
15. Построение АФЧХ ИС по решетчатой импульсной переходной функции.
Передаточная функция разомкнутой ИС может быть получена из решетчатой импульсной переходной функции с помощью выражения:
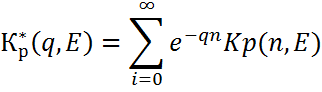
При
замене 
получаем выражение комплексной передаточной функции, для
построения АФЧХ задаемся значениями 
от 0 до П на основании свойств комплексной передаточной
функции.
16. В чем состоит методика определения критического коэффициента с использованием критерия Гурвица?
Характеристическое уравнение:а0 рn+а1 рn-1+...+аn-1 р+аn=о
Для нахождения Ккр составляют главный определитель Гурвица, в котором вместо an элемента делают замену:
an=Kкр – для астатических систем
an=Kкр+1 – для статических систем
В результате решения получаем уравнение, а решив его находим Ккр.
Если главный определитель Гурвица=0, система находится на границе устойчивости, и К=Ккр.
17. Свойства комплексной передаточной функции ИС.
1.
Комплексная передаточная функция разомкнутой ИС является периодической с Т-2П,
т.к. при замене eqq=cos + jsin /
2. АФЧХ разомкнутой ИС начинается и заканчивается на действительной оси.
3. Т.к. комплексная передаточная функция является функцией параметра Е, то для одной и той же ИС можно построить множество ЧХ, зависящих от величины Е, где 0≤Е≤1, то как правило ЧХ строят при Е=0.
18. Дать определения нелинейностей [0; k] и [0;∞).
Нелинейность [0;∞) – НЭ, у которого статическая характеристика проходит через начало координат и укладывается в прямых углах, образованных осями Х и У, вся лежит в 1 и 3 квадраНтах.
Внутри этого подкласса выделяется более узкий подкласс нелинейности [0; k] – подкласс нелинейности, у которого статическая характеристика лежит в острых углах, образованных осью Х и лучом, проходящим через начало координат с угловых коэффициентом К и вся лежит в 1 и 3 квадраНтах.
19. Построение статической характеристики последовательного соединения четырех звеньев. Дать определение статической характеристики.
Статическая характеристика – зависимость выходной величины от входной в установившемся режиме.
Передаточная функция последовательного соединения = произведению передаточных функций всех звеньев.
Сначала ищем статическую характеристику последовательного соединения 3-х звеньев, потом в 1 квадранте рисует сумму 3-х, во втором квадранте рисуем характеристику 4-го элемента, в третьем квадранте – биссектриса, в четвертом квадранте – сумма.
20. Записать передаточные функции замкнутой импульсной системы и относительно ошибки.
относительно изображений дискретного преобразования Лапласа:
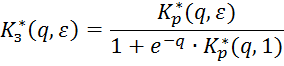
относительно задающего воздействия:
со
скачком: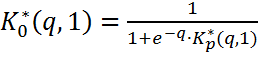
без
скачка: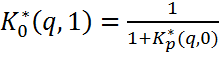 
21. Теорема обычного преобразования Лапласа.
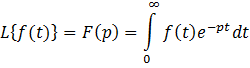
52. Теорема дискретного преобразования Лапласа
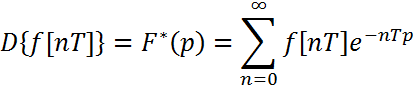
23. Дискретные системы. Определения.
Дискретная система – система, содержащая хотя бы 1 дискретный элемент.
Дискретный элемент – элемент автоматики, работающий не неперывно, а с некоторым периодом, т.е. в импульсном режиме. Выходная величина этого элемента представляет импульс, параметры которого зависят от величины входного сигнала.
Параметры импульса: 1. Амплитуда, 2. Длительность, 3. Интервал чередований.
Непрерывная часть – любое соединение известных непрерывных элементов.
Области применения ДС: радиопоказания, рентген излучение, большая инерционность.
24. Достоинтсва и недостатки дискретных систем.
Достоинства: 1. Один регулятор действия может работать с несколькими объектрами путем поочередного включения.
2. ДС работают с Д информацией, при передачи которой высокая скорость и точность.
3. Имеется возможность включения ЦВМ, что позволяет высокая точность расчетов оптимальных настроек регулятора.
4. Техническое исполнение ДС проще, чем непрерывных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.