Список экзаменационных вопросов с ответами на № 1-51 по дисциплине "Теория автоматического управления" (Порядок нахождения колебательности и степени устойчивости импульсной системы. Корневые показатели качества), страница 2

Для нахождения колебательности в характеристическом уравнении относительно w делаем замену , приравниваем полученное характеристическое уравнение к 0, делаем преобразования, в результате получаем систему двух уравнений: уравнение мнимой части и вещественной, решаем систему уравнений, находим колебательность.

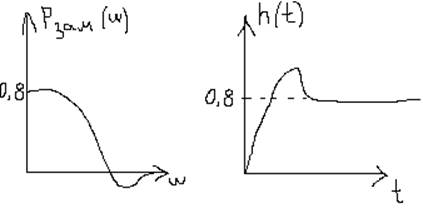
2.  Построение ВЧХ замкнутой системы по годографу Найквиста.

В передаточной функции замкнутой системы делаем замену p=jw, выделяем вещественную и мнимую части, подставляем эти значения в Wзам(jw),  откуда выделяем вещественную часть замкнутой системы

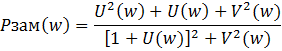
Пользуясь этим выражением на готовой АФХ разомкнутой системы для каждой частоты w последовательно снимают значения U(w) и V(w), рассчитывают Рзам(w) и строят ВЧХ замкнутой системы.

3. Как используются теоремы о конечном и начальном значении оригинала в методе трапеций (пример)?

На основании теоремы о начальном и конечном значении оригинала преобразования Лапласа:

4. Математическая запись метода динамического программирования и порядок решения задач теории оптимального управления с применением метода.

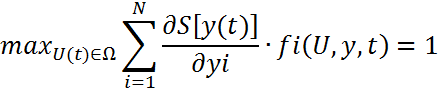
U – оптимальный закон управления

у – оптимальная траектория,

S – минимальное время перехода из у в УК.

N – количество переменных

Порядок решения:

1. Находим изохроны на отдельных интервалах. Изохроны – геометрическое место точек, из которых время попадания в некоторую заданную точку одинаково.

2. Составляем уравнение изохронны.

T[y(t)]=const или S[y(t)]=const

3. Берем частные производные дS[y(t)]/дy

4. Составляем сумму, которая должна быть равна 1.

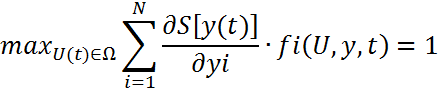
Если сумма не равна 1, то y(t) снова разбивается на интервалы и т.д.

5. В чем заключается методика определения устойчивости импульсной системы с использованием критерия устойчивости Михайлова? Привести формулировку критерия.

Аналог критерия Михайлова для ИС:

имеется характеристическое уравнение относительно параметра z, для построения годографа делаем замену , получаем характеристический вектор, задаваясь значениями от 0 до Пи на комплексной плоскости строим годограф Михайлова этого вектора.

Формулировка:

ИС устойчива, если при изменении w от 0 до Пи характеристический вектор повернется в положительном направлении, т.е. против часовой стрелки на угол nП, где n -  порядок характеристического уравнения.

Если годограф пройдет через начало координат – система нейтральна.

6. Объяснить АИМ 1 и АИМ 2 рода (пример).

Различают 3 вида импульсной модуляции: амплитудно-импульсная АИМ, широтно-импульсная ШИМ, временно-импульсная ВИМ.

АИМ бывает 1-го и 2-го рода.

АИМ 1-го рода: амплитуда импульса постоянна на протяжении всего времени действия импульса и равна значению входного сигнала непосредственно в момент квантования.

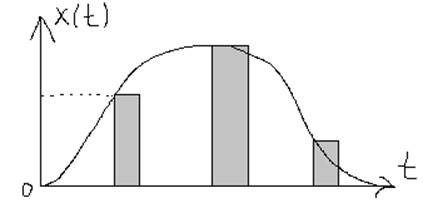
АИМ 2-го рода: амплитуда импульса меняется и повторяет изменение непрерывного входного сигнала в течение всего времени действия импульса.

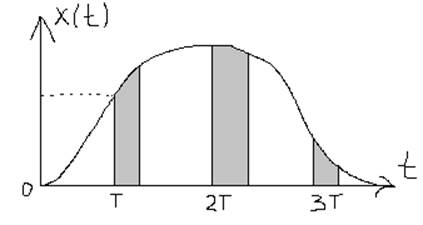
А=f(xвх)

τ=const       ЧИТАЙ :ТАУ РАВНО КОНСТАНТЕ

7. Математическая запись принципа максимума. Объяснить все входящие обозначения.

U – оптимальное управление,

 - вспомогательная ненулевая непрерывная функция ЧИТАЙ ВИЛКА

у – оптимальная траектория

 - допустимая область возможных управлений. ЧИТАЙ ПОДКОВА

8. Что такое эквивалентный импульсный элемент? Дать определения.

Это гипотетическое устройство, т.е. его на самом деле в природе не существует, он выдает последовательность импульса в виде дельта-функций, высота импульсов бесконечно большая величина, длительности импульсов бесконечно малая, площадь которых равна значению входного сигнала в момент времени непосредственно предшествующий импульсу.  Используется для упрощения анализа импульсной системы с АИМ.

9. В чем заключается вычисление интегральных оценок качества для импульсных систем?

Интегральные оценки исследования качества ИС, по аналогии с линейными системами, позволяют оценить длительность переходного процесса и суммарные отклонения регулируемой величины от установившегося значения.