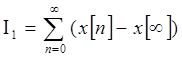 - аналог первой интегральной
оценки;
- аналог первой интегральной
оценки;
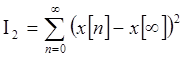 - аналог квадратичной интегральной
оценки,
- аналог квадратичной интегральной
оценки,
![]() -
установившееся значение регулируемой величины (либо
сигнал ошибки, либо статическое отклонение):
-
установившееся значение регулируемой величины (либо
сигнал ошибки, либо статическое отклонение):
![]() .
.
В ИС часто ![]()
![]() .
.
Поэтому
используют: 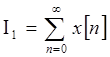
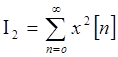
![]() определяет
площадь, заключенную между графиком ступенчатой функции, образующейся из
решетчатой функции
определяет
площадь, заключенную между графиком ступенчатой функции, образующейся из
решетчатой функции ![]() , и графиком ее
установившегося значения (т. е. площадь отклонения ступенчатой функции от ее
предельного значения).
, и графиком ее
установившегося значения (т. е. площадь отклонения ступенчатой функции от ее
предельного значения).
![]() применяется
только для неколебательных процессов.
применяется
только для неколебательных процессов.
Нахождение 1-ой интегральной оценки:
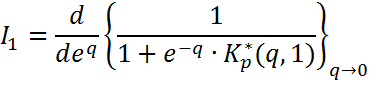
или z=eq
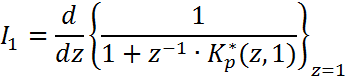
![]() можно
использовать для любых процессов.
можно
использовать для любых процессов. ![]() вычисляют
непосредственно по коэффициентам передаточной функции замкнутой ИС.
вычисляют
непосредственно по коэффициентам передаточной функции замкнутой ИС.
![]() также
можно определить по частотной характеристике замкнутой ИС:
также
можно определить по частотной характеристике замкнутой ИС:
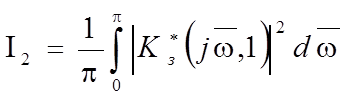
10. Перечислить требуемые показатели качества для построения желаемой ЛАЧХ, что они позволяют определить (построить)?
Желаемой называют асимптотическую ЛАЧХ разомкнутой системы, которая имеет желаемые статические и динамические свойства. Для построения необходимо:
1. статическая ошибка, порядок астатизма.
2. время регулирования и перерегулирование.
Статическая ошибка используется при построении участка низких частот желаемой ЛАЧХ, т.к. для статической системы коэффициент К находят:
![]()
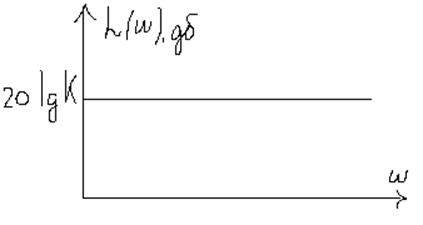
Для астатических систем участок низких частот строят через точку w=1.
Время регулирования и перерегулирования требуется при построении участка средних частот, т.к. они требуются для нахождения частоты среза.
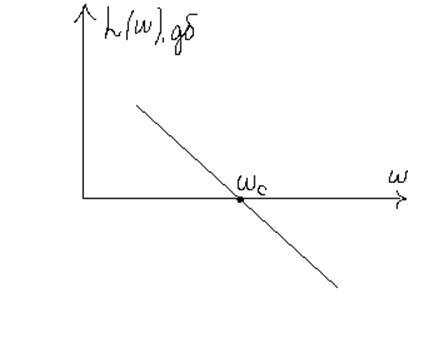
11. Применение частотного критерия для определения устойчивости автоколебаний. Формулировка правила Гольдфарба.
Из частотного критерия устойчивости известно, что автоколебания буду иметь место, если АФЧХ разомкнутой системы проходит через точку (-1;j0). Поэтому при наличии автоколебаний в НС можно записать:
![]()
Это уравнение можно решить графически: на комплексной плоскости строят АФЧХ линейной части и обратную амплитудную характеристику НЭ по выражению
![]()
Наличие точки пересечения АФЧХ ЛЧ и ОАХ НЭ говорит о том, что в данной НС есть автоколебания.
Для определении устойчивости автоколебаний задается некоторое приращение ±Δа, тогда амплитуда будет А=Ад±Δа.
Правило Гольдфарба:
Если АФЧХ ЛЧ не охватывает точку обратной амплитудной характеристики НЭ при увеличении амплитуды до значения А=Ад+Δа, то исследуемые автоколебания устойчивые, и наоборот: точка Ад-Δа должна быть охвачена АФЧХ ЛЧ для устойчивости.
Оси: ось Х – Р(w), Рн(а). Ось У – jQ(w), Qн(а)
12. Формулировка принципа максимума Понтрягина. Как найти u(t) и Ψ(t)?
для оптимального управления U(t) с координатами U1(t), U2(t) и т.д. и оптимальной траектории y(t) с координатами y0(t), y1(t), y2(t) и т.д. необходимо существование ненулевой функции Ψ(t) с координатами Ψ0(t), Ψ1(t), Ψ2(t) и т.д. такой, что для любого значения времени t из интервала от t0 до Т функция Гамильтона H | Ψ(t), U(t), y(t) | при оптимальном управлении U(t) из области возможных управлений достигала бы максимума (U(t) принадлежит некоторой допустимой области возможных управлений подкова)
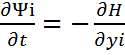 , i=0,1,2…
, i=0,1,2…
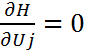 , j=0,1,2…
, j=0,1,2…
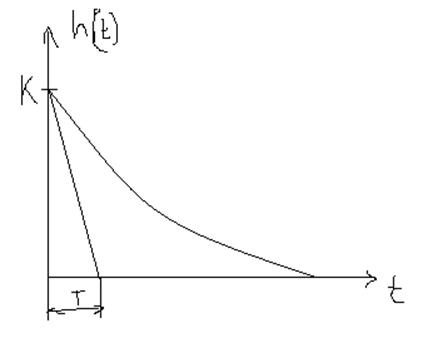
13. Найти единичную переходную функцию реального дифференцирующего звена с параметрами К=2 и Т=2с.
Единичная переходная функция h(t) – реакция звена на единичное ступенчатое воздействие.
h(p)=W(p)*1/p=KTp/Tp+1 * 1/p = K/p+1/T
Используем обратное преобразование Лапласа
h(t)=K*e-1/T*t
14. Сформулировать две теоремы Ляпунова.
1-ая теорема: если корни характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.
2-ая теорема: если среди корней характеристического уравнения первого приближения есть один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.