– Проектирование линейно–квадратичных регуляторов (LQR);
– Характеристики моделей: управляемость, наблюдаемость, понижение порядка модели;
– Поддержка систем с запаздыванием.
Пакет часто используется совместно с другими пакетами MATLAB для проектирования более сложных СУ.
Для нахождения оптимальных настроек регулятора используем пакет «Simulink Response Optimization». В пакете «Simulink» создаём модель объекта (последовательно подключая пиктограммы – «Transfer Fcn» – передаточной функции и «Transport Delay» – запаздывания), присоединим блок «PID–Controller», на вход системы подаем ступенчатое воздействие, для этого подсоединим ко входу системы блок «Step», а к выходу подсоединяем блок графической оболочки оптимизации «Signal Constraint» и графический дисплей – блок «Scope», а также нам понадобится блок «Simout» для вывода данный в рабочее окно MatLab. Схема собранная в пакете «Simulink» представлена на рисунке 9.
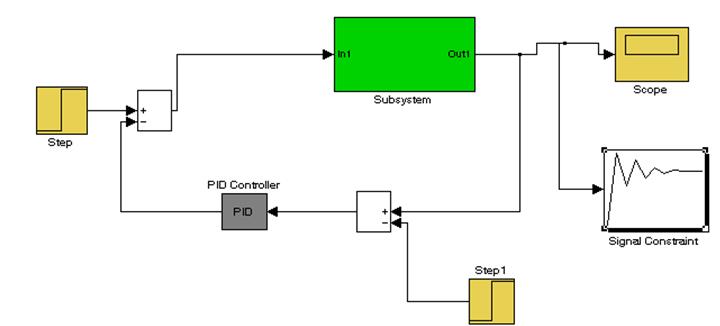
Рисунок 9 – Схема АСС собранная в пакете «Simulink»
Задаем начальные значения параметров ПИД–регулятора в рабочем окне MATLAB 7.0.1, а именно, коэффициенты:
– коэффициент пропорциональной составляющей
Кп = Кр=338,5;
–коэффициент интегральной составляющей
Ки=Кр/Ти=338,5/6,817=49,66;
– коэффициент дифференциальной составляющей
Кд=Кр·Тд=338,5∙1,136=384,536.
Переходной процесс с рассчитанными настройками ПИД–регулятора изображен на рисунке 10.
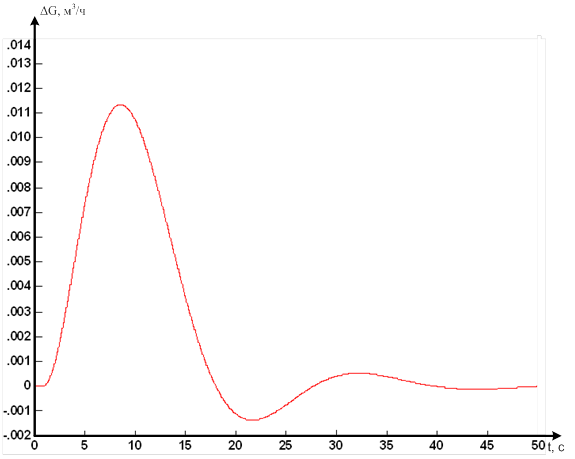
Рисунок 10 – Переходной процесс с рассчитанными настройками ПИД–регулятора
Далее двойным щелчком мыши открываем окно «Block Parameters: Signal Constraint», на представленном поле задаем нужные требования к переходному процессу, путем передвижения красных границ. Следующим этапом наших действий будет указание в меню «Optimizations/Tuned Parametrs» необходимых изменяемых параметров, а именно, в данном случае это рассчитанные ранее коэффициенты Kп, Kи, Kд ПИД–регулятора.
Следующим шагом проводим оптимизацию параметров, для этого нажимаем Start в меню «Optimizations», либо производим это нажатием мышкой по одноименной пиктограмме расположенной под главным меню окна «Block Parameters: Signal Constraint». В результате проведенной оптимизации в окне «Optimization Progress» получаем оптимизированные параметры регулятора, а именно:
– коэффициент пропорциональной составляющей:
Кп = Кр = 1111,5;
– коэффициент интегральной составляющей
Ки = Кр/Ти = 165 и Ти = 6,736;
– коэффициент дифференциальной составляющей
Кд = Кр·Тд = 1310 и Тд = 1,179.
Переходной процесс с оптимальными настройками ПИД–регулятора изображен на рисунке 11.
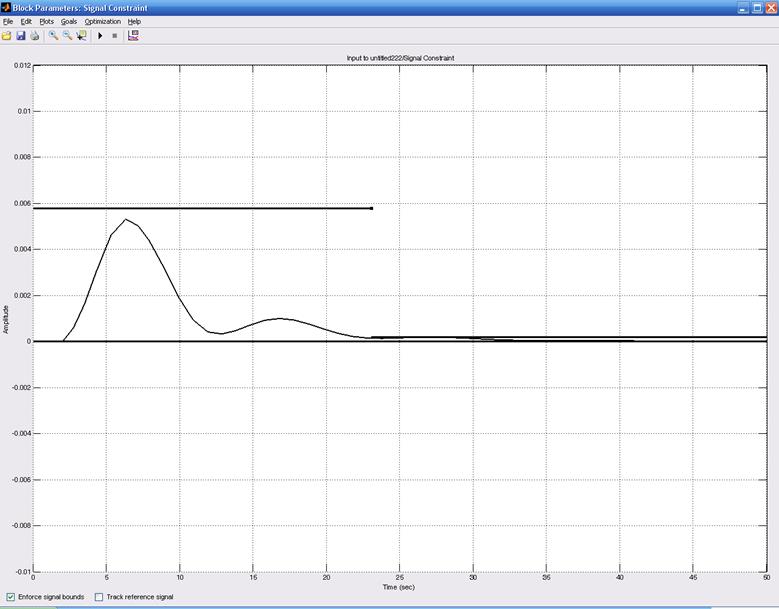
Рисунок 11 – Переходной процесс с оптимальными настройками ПИД – регулятора
Построим переходной процесс с рассчитанными значениями ПИД-регулятора в программном продукте VisSim 6.0 (рисунок 12) и определим его параметры.
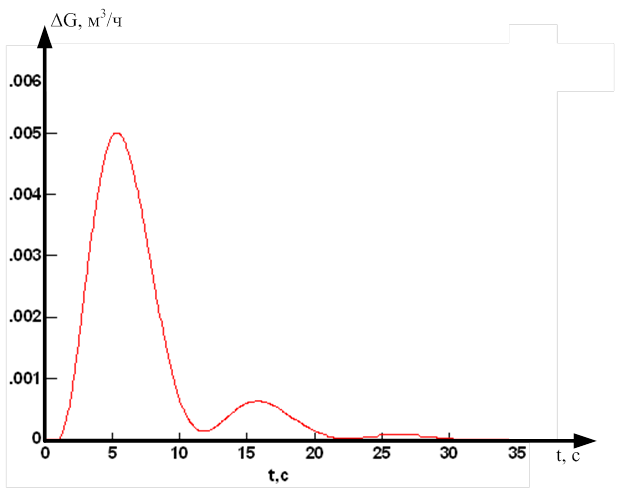
Рисунок 12 – Переходной процесс, построенный в ПП VisSim
Параметры переходного процесса:
– максимальное динамическое отклонение:
ΔG1= 0.005 м3/ч;
– статическая ошибка:
ΔGст= 0;
– время регулирования:
tр= 20 с;
– перерегулирование:
η=0.
В результате проведенных расчетов были получены настройки регулятора позволяющие достигнуть заданных показатели качества переходного процесса.
После расчета настроек регулятора определим запас устойчивости системы по модулю и по фазе, используя частотный критерий Найквиста-Михайлова.
Для этого рассчитаем АФЧХ объекта и регулятора, которую получают подстановкой p=jωв передаточную функцию.
Определяем сначала АФЧХ объекта:
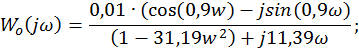
Разделим выражение Wо(jω) на вещественную и мнимую части. Для этого умножим числитель и знаменатель Wо(jω) на комплексно–сопряженное знаменателю выражение:
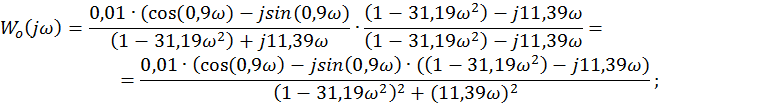
Выражения для вещественной Po(ω) и мнимой Qo(ω) частей равны:
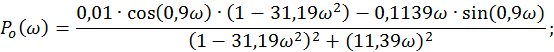
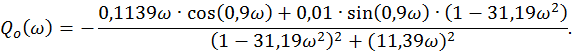
Далее рассчитаем АФХ ПИД–регулятора:
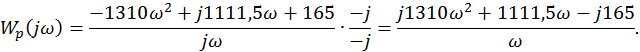
Разделив Wp(jω) на вещественную и мнимую части, получим:
![]()
![]() .
.
АФЧХ разомкнутой системы получим как произведение АФХ объекта Wо(jω) и регулятора Wp(jω):
![]()
![]() .
.
Разделим Wраз(jω) на вещественную и мнимую части:
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.