Исследование вопросов по автоматизации процесса экстракционного извлечения урана из активного раствора, а именно – автоматизация экстрактора ЭКЦГ-140, страница 12

Окончание таблицы 2

По результатам таблицы 2 построим экспериментальную ∆G(t), единичную ∆G⁰(t) и нормированную ∆G^н(t) переходные характеристики, рисунок 5.

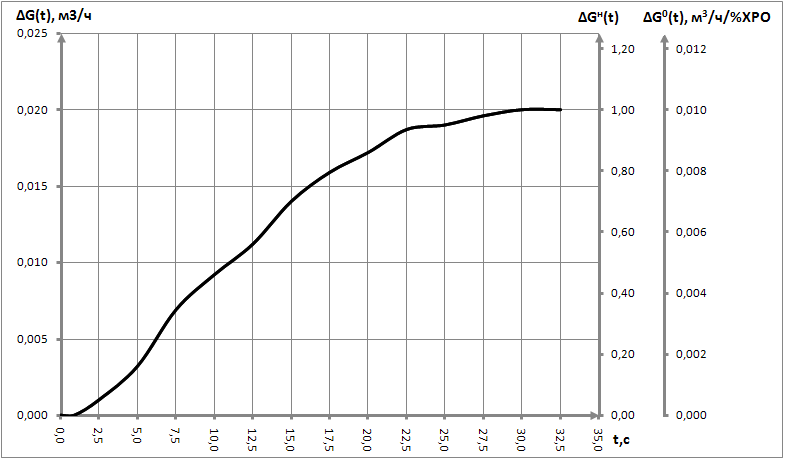
Рисунок 5 – Переходные характеристики: ∆G(t) – переходная характеристика, полученная экспериментально;  ∆G⁰(t) – единичная переходная характеристика; ∆G^н(t) – нормированная переходная характеристика

Коэффициент усиления объекта равен:

К_об
=∆G⁰(T_у)=0,01 (м³/ч)/%ХРО.

При аппроксимации объекта последовательным соединением апериодического звена и звена чистого запаздывания определяем его динамические характеристики, для этого отметим на графике нормированной переходной характеристики (рисунок 6) точки А и Б, такие, что ∆G^н(t_А)=0,10, ∆G^н(t_Б)=0,70, получим t_А=3,9-0,9=3,0с, t_Б=15-0,9=14,1с.

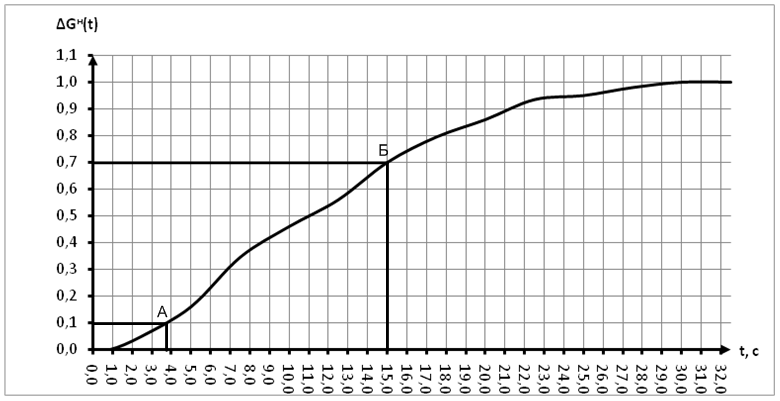
Рисунок 6 – Нормированная переходная характеристика

Находим дополнительное запаздывание:

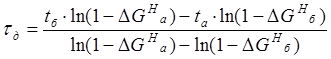                      ,                                          (3)

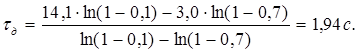
Общее запаздывание объекта:

,                                                                                                        (4)

;

 и постоянную времени

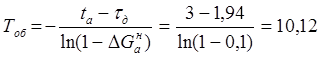                               с.                                  (5)

Таким образом, передаточная функция объекта имеет вид:

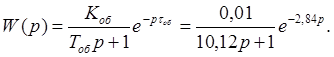                            (6)

Для определения точности аппроксимации экспериментальной переходной функции решением дифференциального уравнения первого порядка с запаздывающим аргументом рассчитываем ординаты аппроксимирующей кривой:

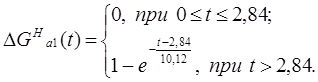,                                                                   (7)

Результаты расчетов приведены в таблице 3, а нормированная и аппроксимирующая нормированная кривые показаны на рисунке 7.

Таблица 3 – Ординаты аппроксимирующей нормированной переходной функции

Окончание таблицы 3

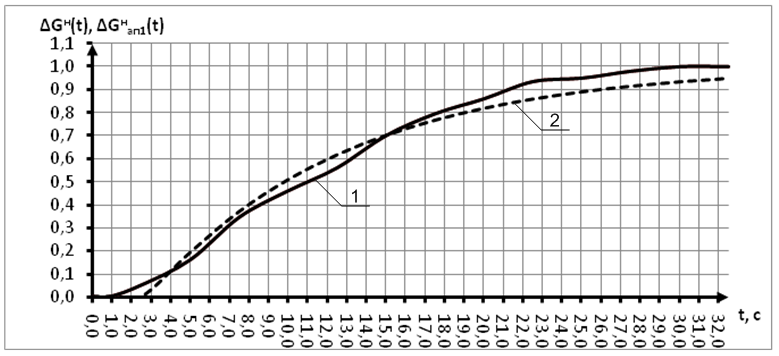
Рисунок 7 – График переходных функций: 1 – нормированная, снятая экспериментально,  2 – нормированная, построенная по  первой аппроксимации

Найдем среднеквадратическую ошибку аппроксимации:

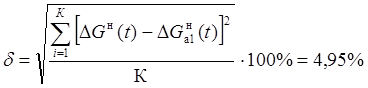,                          (8)

где К – число точек нормированной и аппроксимирующей кривой, К=14.

Так как ошибка аппроксимации больше 3%, осуществляем аппроксимацию объекта последовательным соединением двух апериодических звеньев и звена запаздывания (решением дифференциального уравнения второго порядка с запаздывающим аргументом).

Определение параметров передаточной функции осуществляем по нормированной переходной характеристики [3, с. 92].

Находим относительное время:

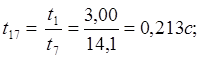                                                              (9)

Приняв n=1, по нормированной переходной характеристики определяем относительные значения постоянных времени: Т^*₁=0,483; Т^*₂=0,325.