Исследование вопросов по автоматизации процесса экстракционного извлечения урана из активного раствора, а именно – автоматизация экстрактора ЭКЦГ-140, страница 13

Далее

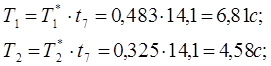                                        (10)

Таким образом, передаточная функция объекта будет иметь вид:

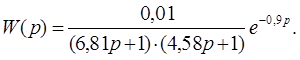
Для определения точности аппроксимации экспериментальной переходной функции решением дифференциального уравнения с запаздывающим аргументом рассчитываем ординаты аппроксимирующей кривой:

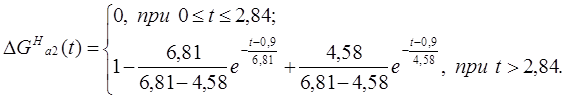,              (11)

Результаты расчетов приведены в таблице 4, а нормированная и аппроксимирующая нормированная кривые показаны на рисунке 8.

Таблица 4 – Ординаты аппроксимирующей нормированной переходной функции

t,c	0,0	0,9	2,5	5,0	7,5	10,0	12,5	15,0
ΔGнап2(t)	0,000	0,000	0,000	0,167	0,327	0,479	0,607	0,709

Окончание таблицы 4

17,5	20,0	22,5	25,0	27,5	30,0	32,5
0,788	0,847	0,890	0,922	0,945	0,961	0,973

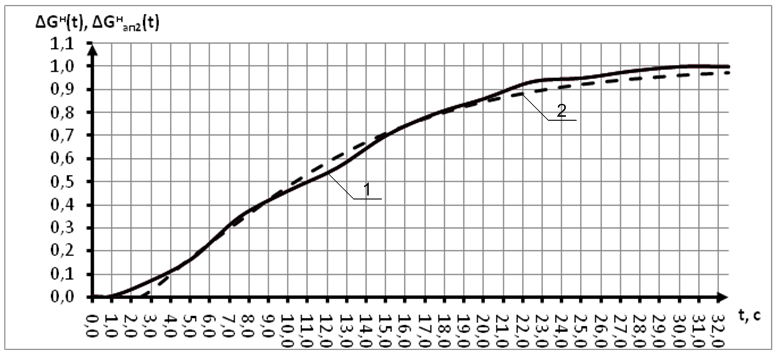
Рисунок 8 – График переходных функций: 1 – нормированная, снятая экспериментально,  2 – нормированная, построенная по  второй аппроксимации

Найдем среднеквадратическую ошибку аппроксимации:

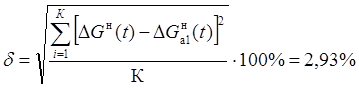,                           (12)

Так как погрешность аппроксимация меньше 3%, окончательно принимаем передаточную функцию объекта в виде:

3.2 Выбор регулятора для АСР расхода экстрагента

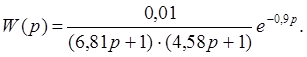
Для выбора закона регулирования (типа регулятора) воспользуемся аппроксимацией объекта решением дифференциального уравнения первого порядка  с запаздывающим аргументом.

По отношению

(13)

из таблицы 2.1 [3] выбираем непрерывный регулятор.

Затем, рассчитываем динамический коэффициент регулирования по формуле:

(14)

По графику (рисунок 2.3 [3]) определяем, что R_д = 0,2 для требуемого вида переходного процесса, а именно, апериодического, может обеспечить ПИД –регулятор.

По графику (рисунок 2.4 [3]), находим для ПИД–регулятора отношение:

.

(15)

Откуда время регулирования t_р=5·2,84 = 14,2 с, что меньше допустимого времени регулирования 24с.

Поэтому окончательно выбираем ПИД – регулятор.

3.3 Определение настроек регулятора и построение переходного процесса АСР расхода экстрагента

Предварительно, с целью определения варьирования настроек, рассчитываем коэффициент передачи регулятора К_р, время изодрома Т_и и время предварения Т_д по приближенным формулам (таблица 2.2 [3]).

Для переходного процесса апериодического:

	(16)

Расчет оптимальных настроек регулятора произведем с помощью пакета прикладных программ MATLAB 7.0.1.

Для построения переходного процесса по заданию воспользуемся программным продуктом MATLAB7 и пакетом ControlSystemToolbox, который является одним из основных инструментариев разработчика систем управления в среде MATLAB 7. Это сборник алгоритмов MATLAB для моделирования, анализа и проектирования СУ. В пакете используются как и традиционные методы ТАУ с использованием передаточных функций, так и современные методы с использованием пространства состояния. В среде ControlSystem Toolboxможно моделировать и анализировать как непрерывные, так и дискретные СУ. Легко могут быть вычислены и отображены на экране отклики системы в частотной и временной областях, диаграммы расположения нулей/полюсов.

Основные свойства пакета ControlSystem:

Формы представления:

– Непрерывные и дискретные СУ;

– Форматы моделей: передаточные функции (ПФ), пространство состояний (ПС), нули-полюса (НП);

– Построение линейных моделей СУ;

– Преобразование моделей в различные форматы: ПФ, НП, ПС.

Анализ:

– Полный набор средств для анализа одно– (SISO) и многомерных (MIMO) систем;

– Временные характеристики: переходная и импульсная переходная характеристики, реакция системы на произвольное воздействие;

– Частотные характеристики: диаграммы Боде (АЧХ, ФЧХ), Найквиста и Никольса (АФХ) и др.

Проектирование:

– Расчет параметров обратной связи;