Оценка мореходных качеств судна: Методические указания по выполнению курсового проекта по дисциплине "Теория и устройство судна", страница 12

Контейнер массой m в соответствии с заданием размещен на крышке грузового люка трюма №2. Центр тяжести контейнера с грузом G находится на ½ высоты контейнера от основания. Необходимые для расчетов размеры показаны на рисунке (рис. 15).

            Определить усилия от сил P_y и P_z в найтовах 1 и 2, развивающиеся при резонансной качке судна с периодом t_к =t_q, для 100% загрузки судна (на отход).

Смещающая и нормальная к палубе силы P_y и P_z определяются по формулам:

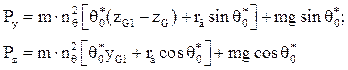
Здесь m – масса груза;

             - резонансная амплитуда бортовой качки судна (п. 4.4);

            z_G1 – аппликата ЦТ контейнера относительно ОП судна;

            y_G1 – ордината ЦТ контейнера относительно ДП судна;

            r_в – амплитуда орбитального движения судна при поперечной качке. Положить ее равной ½ высоты волны с обеспеченностью 0,1% (п. 4.2);

            Углы a₁ и a₂, натяжения найтовов относительно палубы судна равны соответственно: a₁ = 60⁰ и a₂ = 70⁰.

            Привести схему действия сил и получить для них расчетные формулы для двух случаев:

а) в момент наибольшего наклонения судна на правый борт на угол ;

б) в момент наибольшего наклонения судна на левый борт на угол .

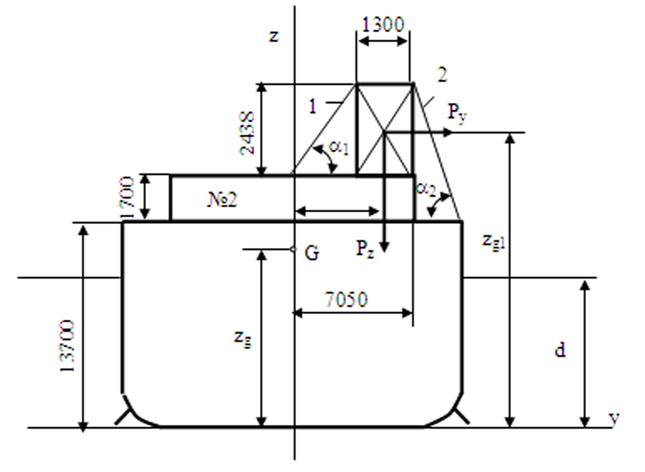
Рис. 15 Схема размещения палубного груза

4.13 Определение скорости судна, опасной в отношении слеминга.

            Для заданной интенсивности встречного волнения (курсовой угол волнения c=0⁰) определить скорость хода, при которой частота ударов судна о воду и вероятность появления слеминга достигнут опасных значений, за которые принимают: p*_сл=0,01, 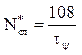(1/ч)                                                             (4.14)

Здесь t_y - период собственной килевой качки при 100% загрузке.

Рассчитать среднюю частоту относительных перемещений носовой оконечности судна:

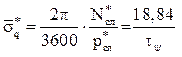 (1/ч)                                                  (4.15)

С другой стороны, величина этой частоты зависит от скорости хода судна (иначе – от числа Фруда) и может быть представлена в виде:

 (1/ч)                                                  (4.16)

Здесь:  - средний период волнения (п. 4.2);

.

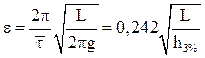Зависимость  представлена на графике рис. 16.

Определив , из (4.16) получить значение k_s (Fr):

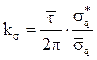                                                                           (4.17)

            Воспользовавшись графиком рис. 17, определить число Фруда Fr*, а по нему - предельную скорость судна

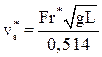 (узл)                                                                  (4.18)

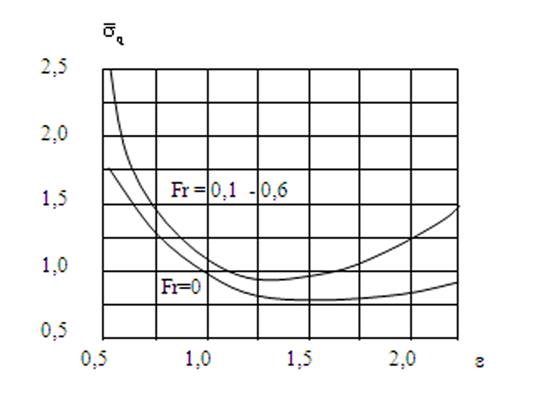
Рис. 16 Относительная характеристика перемещений носовой оконечности при слеминге

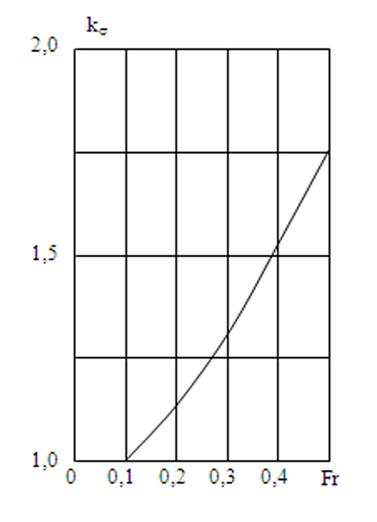
Рис. 17 Зависимость коэффициента k_s от Fr

5. Ходкость судна

5.1 Оценка ходкости судна на мелководье и в канале

При глубине акватории H, в соответствии с заданием, определить следующие характеристики движения судна:

5.1.1 Рассчитать критическую скорость движения судна, исходя из того, что критические значения числа Фруда по глубине имеют значения .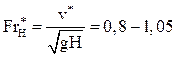

Задаться любым значением числа Фруда из указанного диапазона и определить критическую скорость. Перевести ее значение из м/с в узлы.

5.1.2 Определить допустимую скорость движения судна в канале с такой же глубиной Н исходя из соображений защиты ложа канала от разрушения корабельными волнами. Движение в канале допустимо при значениях числа Фруда .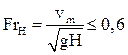

Задаться значением числа Фруда Fr_H =0,6,   определить допустимую скорость. Перевести ее значение из м/с в узлы.

5.1.3 Определить просадку судна dd, движущегося в канале со скоростью v_m (п. 5.1.2) по соотношению:

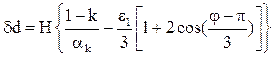                                       (4.19)

Где:  ;

            ;

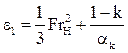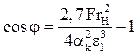             - отношение площади мидельшпангоута судна к площади сечения кнала.

            S = 1400м²;

            a_k – коэффициент, зависящий от формы сечения канала. Для прямоугольного в плане канала равный a_k  = 1,0.

5.1.4 Определить потерю скорости судна dv на мелководье глубиной Н по сравнению со скоростью на глубокой воде по соотношению:

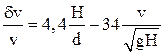                                                             (4.20)

Здесь v – скорость полного хода судна на большой глубине. Эту скорость принять соответствующей эксплуатационной при осадке 10 м (см. Раздел 2 – Технические данные т/х); Скорость и потеря скорости в соотношении (4.20) – в м/с.