Одномерный прямоугольный потенциальный барьер представлен на рис.1.1. В классической механике полная энергия частицы Е является суммой кинетической и потенциальной энергии и всегда постоянна. Если энергия частицы Е меньше величины потенциального барьера U0, то частица не может иметь координаты 0 < x < l. В квантовой механике нет постулата постоянства полной энергии и полная энергия не является суммой кинетической и потенциальной энергий. Эти энергии даже не определяются одновременно. Кинетическая энергия – функция импульса, а потенциальная – функция координат. Полная энергия определяется как собственное значение оператора Гамильтона, а собственные значения волновой функции, описывающей состояние частицы, могут оказаться не равными нулю даже при значениях 0 < x < l, запрещённых классической механикой.
![]() U
U
 |
U0
![]() X
X
0 l
Рис. 1.1. Прямоугольный потенциальный барьер.
Трём участкам рис. 1.1 соответствуют следующие уравнения Шредингера:
![]() x < 0
x < 0 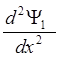 +
+ ![]() E
E![]() =
0;
=
0;
![]() 0
0 ![]() x
x ![]() l
l 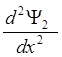 +
+ ![]() (E - U0)
(E - U0)![]() =
0;
=
0;
![]() x > l
x > l
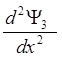 +
+ ![]() E
E![]() = 0.
= 0.
Решения этих уравнений следующие:
![]() ;
;
![]() ;
;
![]() .
.
Где
![]() ,
, ![]() .
.
В области потенциального барьера (0 < x < l) при 0 < E < Uo
![]() , где
, где ![]() .
.
Поскольку
l в ![]() - действительная
положительная величина, а волновая функция при
- действительная
положительная величина, а волновая функция при ![]() должна
оставаться ограниченной, то очевидно, что коэффициент а следует выбрать
равным нулю. Отсюда
должна
оставаться ограниченной, то очевидно, что коэффициент а следует выбрать
равным нулю. Отсюда
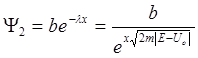 .
(1.35)
.
(1.35)
Т.к.
вероятность обнаружить электрон при каком-либо значении x
равна ![]() , то из последнего выражения видно, что в
области 0 < x
< l
, то из последнего выражения видно, что в
области 0 < x
< l ![]() ¹ 0 и чем больше х
и Uo, тем вероятность нахождения там электрона ниже. В
классической физике при E <
Uo в области 0 <
x <
l вероятность нахождения электрона равна нолю.
¹ 0 и чем больше х
и Uo, тем вероятность нахождения там электрона ниже. В
классической физике при E <
Uo в области 0 <
x <
l вероятность нахождения электрона равна нолю.
Произведя необходимые математические действия, можно
получить коэффициент прозрачности барьера D.
Коэффициентом прозрачности барьера называется отношение величин токов прошедшей
и падающей волн. Если падающая волна де Бройля ![]() , а
прошедшая
, а
прошедшая ![]() , то ток волны определяется выражением:
, то ток волны определяется выражением: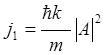 . Отсюда
. Отсюда
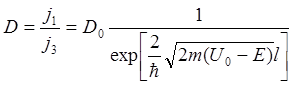 .
(1.36)
.
(1.36)
Из последнего уравнения видно, что чем выше и шире барьер, тем меньше коэффициент прозрачности.
Приведённый расчёт хорошо описывает распад радиоактивных ядер.
1.7.3. Линейный гармонический осциллятор.
В классической механике линейный осциллятор совершает гармонические колебания по закону:
![]() ,
,
где
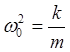 (k –жёсткость
осциллятора, m – масса колеблющейся точки). При этом энергия
осциллятора, оставаясь постоянной во времени, может быть суммой непрерывного
ряда значений составляющих её компонент начиная от нуля:
(k –жёсткость
осциллятора, m – масса колеблющейся точки). При этом энергия
осциллятора, оставаясь постоянной во времени, может быть суммой непрерывного
ряда значений составляющих её компонент начиная от нуля:
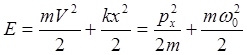 .
.
В квантовой механике состояние осциллятора описывается собственной функцией оператора Гамильтона или соответствующим уравнением Шредингера:
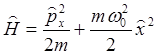 или (1.37)
или (1.37)
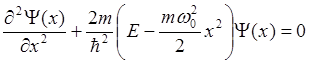 . (1.38)
. (1.38)
Решив уравнение Шредингера, получают собственные функции гамильтониана (эти функции включают в себя полином Чебышева-Эрмита и имеют довольно громоздкий вид); затем определяют собственные значения:
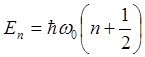 при n = 0, 1, 2,
3, …, (1.39)
при n = 0, 1, 2,
3, …, (1.39)
где n – главное квантовое число. Таким образом, в квантовой механике энергия линейного гармонического осциллятора принимает дискретный ряд значений. Наименьшая энергия квантового осциллятора не равна нулю.
1.8. Экспериментальное подтверждение дискретности динамических параметров микрочастиц. Эффект Зеемана.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.