С позиций классической физики полная энергия системы является суммой кинетической и потенциальной энергий:
Е = 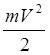 + Еп.
(1.28)
+ Еп.
(1.28)
Выразим кинетическую энергию через импульс. Тогда выражение 1.23 будет выглядеть следующим образом:
Е = ![]() + Еп.
(1.29)
+ Еп.
(1.29)
Если в выражении 1.29 импульс заменить оператором импульса (1.23), представив квадрат функции как вторую производную по координатам, а потенциальную энергию обозначить через V, то получим выражение для гамильтониана:
![]() =
= 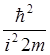 Ñ2 + V
= -
Ñ2 + V
= - 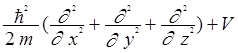 (1.30)
(1.30)
Последнее уравнение справедливо лишь в том случае, когда силы, действующие на частицу, не зависят от времени. Однако в электромагнитном поле возникает сила Лоренца, которая зависит от скорости частицы:
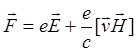 , (1.31)
, (1.31)
где e
– заряд частицы, ![]() и
и ![]() -
напряжённости электрического и магнитного полей соответственно, v
– скорость движения частицы, c – скорость света. Если векторы напряжённостей
заменить скалярным потенциалом j и векторным
потенциалом
-
напряжённости электрического и магнитного полей соответственно, v
– скорость движения частицы, c – скорость света. Если векторы напряжённостей
заменить скалярным потенциалом j и векторным
потенциалом ![]() , то в общем случае оператор Гамильтона
имеет вид:
, то в общем случае оператор Гамильтона
имеет вид:
![]() =
= 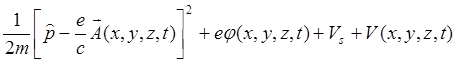 .
(1.32)
.
(1.32)
В
ур.1.32 член ![]() описывает
взаимодействие спина электрона с магнитным полем, а член V(x,y,z,t) учитывает возможность наличия другого, не
электромагнитного поля.
описывает
взаимодействие спина электрона с магнитным полем, а член V(x,y,z,t) учитывает возможность наличия другого, не
электромагнитного поля.
1.5. Соотношение неопределённости. Квантовая механика Гейзенберга.
1.5.1. Соотношение неопределённости.
Использование волнового уравнения для описания состояния электрона приводит к тому, что как и для любой плоской волны амплитуда состояния всюду имеет одинаковое значение. Т.е. частицу можно найти в любой точке пространства с одинаковой вероятностью – положение частицы неопределено. С другой стороны, с некоторой точностью мы всегда можем говорить о положении микрочастицы в некоторой области пространства Dt. И, если положение частицы описывать с помощью волновой функции, то тогда мы должны говорить о волновом пакете. Волновой пакет можно себе представить как наложение гармонических волн, которые в результате интерференции усиливают друг друга в небольшой области Dt, а вне её полностью погашаются.Но чем меньше размер Dt (волнового пакета), тем шире спектральный интервал (из интеграла Фурье) и тем менее определено состояние движения (например, импульс) частицы.
Принципиальным отличием в описании движения частиц в квантовой механике по отношению к классической является то, что в квантовой механике нет точной траектории движения. С помощью волнового уравнения мы можем получить только вероятность нахождения частицы в какой-либо точке пространства. Степень этой неопределенности можно оценить по соотношению, предложенному немецким физиком-теоретиком Гейзенбергом в 1927 г.:
Dx×Dpx ³ ![]() ,
(1.33)
,
(1.33)
где Dx и Dpx – погрешности в определении координаты и импульса. Данное соотношение справедливо и для других, канонически сопряжённых между собой переменных:
DE×Dt ³ ![]() , Dj×DМ ³
, Dj×DМ ³ ![]() ,
,
где DE, Dt, Dj, DМ – погрешности в определении энергии, времени, угла и момента количества движения соответственно.
В принципе построение теории может быть равноправно
проведено либо для точного значения координат, либо для точного значения
энергии. В квантовой химии все рассуждения и вычисления производятся для
случая, когда энергия (и импульс соответственно) точно определена, а
координата неопределена. Это связано с тем, что экспериментально значительно
легче измерить энергию частицы, чем ее положение в пространстве. Для частиц с
большой массой (m ® µ) произведение Dx×DV ³ ![]() ® 0 и мы переходим к законам классической физики.
® 0 и мы переходим к законам классической физики.
1.5.2. Квантовая механика Гейзенберга.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.