1. ОСНОВНЫЕ ПОНЯТИЯ
1.1. Волновая функция.
Волновая функция - это функция состояния электрона (электронов или других элементарных частиц), которая полностью определяет динамические свойства системы. Волновая функция зависит от координат и времени. В общем виде функция состояния системы (волновая функция) записывается в следующем виде
Y(q1, q2 ... qn, t).
Часто зависимость от времени исключают (Y(q1, q2 ... qn)). Здесь аргументы q1, q2 ... qn есть координаты пространства и проекция спина одной или нескольких микрочастиц. При этом в отличие от классической механики координаты xi, yi, zi рассматриваются не как функция времени, а как независимые переменные. В квантовой механике волновую функцию находят путем решения волнового уравнения (в частности уравнения Шредингера). При этом применяют только регулярные функции, т.е. функции, подчиняющиеся следующим условиям:
1. Конечность во всем пространстве. В противном случае невозможно определить параметры системы в тех точках, где волновая функция обращается в бесконечность.
2. Однозначность. В любой точке пространства функция принимает одно единственное значение.
3. Непрерывность. Нет разрывов. Функция определена при любых значения аргументов.
В качестве примера рассмотрим волновую функцию для свободного электрона, которая описывает состояние плоской монохроматической волны, распространяющуюся вдоль координаты X
Y = 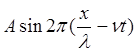 (1.1)
(1.1)
где l - длина волны, n - частота. В зависимости от начальных граничных условий вместо sin может быть cos. В случае стоячей волны вид функции принимает вид
Y=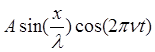 или Y=
или Y=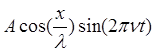 .
(1.2)
.
(1.2)
В приведенных записях учитывается как положение в пространстве, так и зависимость от времени. В дальнейшем мы будем иметь дело только с функциями, не зависимыми от времени.
В
квантовой механике волновая функция ![]() представляет собой
амплитуду распределения вероятности положения частицы (аналог амплитуды для волнового движения в
классической механике). Вероятность найти
частицу около точки x -
представляет собой
амплитуду распределения вероятности положения частицы (аналог амплитуды для волнового движения в
классической механике). Вероятность найти
частицу около точки x - ![]()
![]() =
=![]() , а в
объеме dt -
, а в
объеме dt - ![]() .
.
Отметим некоторые свойства волновых функций. Так, если Y - решение волнового уравнения, то и Y1 = СY (где С - константа) является решением этого волнового уравнения.
Другим свойством волновой функции является принцип суперпозиции. Если система может находиться в состояниях, описываемых волновыми функциями Y1 и Y2 (решения волнового уравнения), то она может находиться и в состоянии Y = aY1 + bY2. где a и b простые числа (т.е. Y также решение исходного уравнения). Это легко показать подстановкой новой волной функции в исходное волновое уравнение.
Примером принципа суперпозиции является волновая функция свободного электрона
Y = A(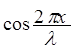 +
+ 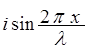 ) = A
) = A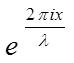 .
(1.3)
.
(1.3)
Используя принцип суперпозиции можно получить волновые функции для p-состояния атома (три независимые друг от друга функции).
Y+1
= (x + iy)![]() ;
(1.4)
;
(1.4)
Y-1 = (x - iy)![]() ; (1.5)
; (1.5)
Yo = z![]() ,
(1.6)
,
(1.6)
где ![]() -
сферически симметричная волновая функция (соответствует s-состоянию
атома).
-
сферически симметричная волновая функция (соответствует s-состоянию
атома). ![]() = e-ar.
= e-ar.
При
расчётах в квантовой химии используют нормированные волновые функции.
Нормировка волновой функции заключается в определении нормировочного множителя
(множителей). Произведём нормировку волновой функции, соответствующей s-электрону в атоме, Y = ![]() , т.е.
определим множитель С.
, т.е.
определим множитель С.
Условие
нормировки: ![]() .
.
![]() ;
; 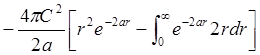 =
=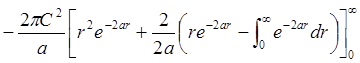 =
=
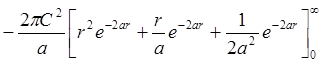 =
=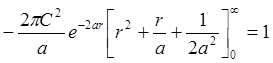
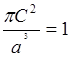 ;
; 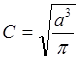 .
.
4. Ортогональность волновых функций. Важным свойством волновых функций, используемых в квантовой химии, является их ортогональность.
Условие ортогональности имеет вид:
![]() .
(1.7)
.
(1.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.