Как известно Гейзенберг создал свой аппарат квантовой механики. Он считал, что раз мы не можем непосредственно наблюдать положение, скорость или траекторию атомных электронов, то не следует эти понятия вводить и в новые теоретические положения. Единственно, что нам известно об атоме – это параметры его стационарного состояния, переходы между ними и излучения, которые сопровождают эти переходы. Поэтому Гейзенберг составил матрицы, элементами которых были реально наблюдаемые величины. Диагональные элементы этих матриц описывают стационарные состояния. Недиагональные элементы c разными индексами описывают переходы между стационарными состояниями, соответствующими этим индексам. Что же касается величины этих элементов, то их можно связать по формулам, полученным с помощью принципа соответствия, с величинами, характеризующими излучение при этих переходах.
Важно отметить, что при перемножении матрицы, соответствующей координате, на матрицу, соответствующую канонически сопряжённой компоненте импульса, порядок множителей не безразличен (матрицы не коммутируют) и что разность между произведением этих двух величин, взятых в одном порядке, и их произведением в противоположном порядке (определитель матрицы) равна постоянной Планка h, умноженной на некоторое число.
Все другие канонические переменные квантовой механики коммутируют между собой. В макроскопических явлениях, где величиной h можно пренебречь, все механические величины можно считать коммутирующими.
1.6. Определённые и неопределённые величины.
Как
уже говорилось выше, в квантовой механике одни величины, характеризующие
состояние частицы, точно определены, а другие не имеют точного значения. Есть
возможность выяснить к какой из этих групп относится искомая величина. Для
этого необходимо подействовать соответствующим оператором на волновую функцию.
Если в результате такого действия получится та же волновая функция, умноженная
на постоянную величину, то этот параметр имеет точное значение (мы получим
произведение собственного значения на собственную функцию оператора). Например: воздействуем
оператором импульса по оси Х на волновую функцию s-электрона
(![]() =
=![]() ):
):
![]()
![]() Ys =
Ys = 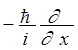
![]() =
=
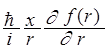 = -
= -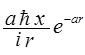 ;
;
![]() - переменная величина (неопределена),
следовательно импульс для s -электрона неопределен.
- переменная величина (неопределена),
следовательно импульс для s -электрона неопределен.
Произведем ту же операцию с волновой функцией свободного электрона:
![]() Ye
=
Ye
= 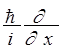
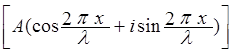 =
=
![]()
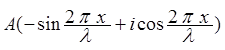 =
= ![]()
![]()
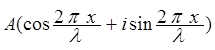 = pYe.
= pYe.
Здесь
р (![]() ) - собственное значение, а Ye -
собственная волновая функция оператора импульса. Таким образом, для свободного
электрона импульс определен и имеет значение
) - собственное значение, а Ye -
собственная волновая функция оператора импульса. Таким образом, для свободного
электрона импульс определен и имеет значение ![]() .
.
Лекция 3
1.7. Решение волнового уравнения для некоторых частных случаев одномерного движения частицы.
1.7.1. Движение в одномерной потенциальной яме с бесконечно высокими стенками. Дискретные квантовые состояния.
Рассмотрим
движение электрона вдоль оси X между двумя отражающими стенками, т.е. в
так называемом потенциальном «ящике». В этом случае частица находится в поле
потенциала вида V(x) = 0, если
0 < x<
L, и V(x) = ![]() в других точках. Соответственно Yо = 0 и YL = 0
при x = 0 и x=
L. Решением волнового уравнения
в других точках. Соответственно Yо = 0 и YL = 0
при x = 0 и x=
L. Решением волнового уравнения
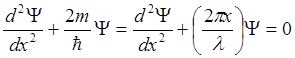
будет
Y = A× sin ![]() , а решение с cos не удовлетворяет
граничному условию.
, а решение с cos не удовлетворяет
граничному условию.
Далее, при х = L Y = 0. Поэтому
sin ![]() = 0 и sin np = 0, то
= 0 и sin np = 0, то ![]() = np,
= np, 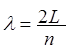 (n - 1; 2; 3 ...).
(n - 1; 2; 3 ...).
И существует бесконечное множество решений:
Yn
= Asin ![]() x.
x.
Значение
коэффициента А в результате решения уравнения Шредингера может быть
произвольным. Однако, если поставить условие, что электрон находится в
некоторой области пространства dt, то А можно
вычислить путём нормировки ![]() . В соответствии с полученным решением энергия электрона
может принимать только определённые значения. Т.к.
. В соответствии с полученным решением энергия электрона
может принимать только определённые значения. Т.к. ![]() =
= ![]() , то из соотношения
, то из соотношения ![]() =
mV следует (
=
mV следует (![]() )2 = (mV)2
;
)2 = (mV)2
; 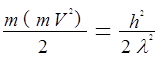 ;
;
En = 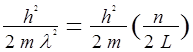 2 =
2 = 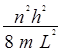 . (1.34)
. (1.34)
Т.о. дозволенные значения энергии электрона соотносятся как n2 и промежуточных значений не может быть. Дискретные значения энергии называют уровнями энергии, а низший уровень – основным. Следующий за основным называют первым возбуждённым уровнем. И так далее.
1.7.2. Движение с прямоугольным потенциальным барьером.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.