Квантовая химия как наука. Математический аппарат в квантовой химии. Решение волнового уравнения для некоторых частных случаев одномерного движения частицы, страница 11

Рис.1.4.  Пространственное квантование и эффект Зеемана для спина электрона.

          В настоящее время спин и его свойства понимаются как необходимое и естественное следствие комбинации теории относительности и квантовой механики. В атомной физике МКД часто изображается соответствующими квантовыми числами. Например, m_z = M_z/ или m_sz = M_sz/.

          1.10. Полный момент количества движения.

          В случае одного электрона полный МКД будет равен геометрической сумме векторов спинового и орбитального МКД вдоль оси Z: j = l + s. Значение j определяет число энергетических подуровней атома в магнитном поле, которое равно 2j + 1. Для р-электрона  при j_max = 3/2 j принимает следующие значения: +3/2, +1/2, -1/2 и -3/2, а при j_max = 1/2 : +1/2 и -1/2. В первом случае говорят о четырехкратном вырождении уровня МКД, а во втором – о двукратном. Для d-электрона при j_max = 5/2 имеет место шестикратное вырождение, а при j_max = 3/2 – четырехкратное. Схемы расщепления уровней для p- и d-состояний электрона представлены на рис.1.5.

В действительности энергетические состояния с разными значениями j отличаются по энергии и в отсутствии внешнего магнитного поля. Расщепление возникает за счет взаимодействия спинового и орбитального магнитных моментов электрона. Оценим величину этого взаимодействия. Два магнитных диполя на расстоянии rобладают потенциальной энергией равной

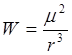.                                                                                             (1.45)

Здесь r - расстояние порядка боровского радиуса

r =.                                                                                          (1.46)

Рис.1.5. Расщепление p- и d-состояний в магнитном поле.

Таким образом, расщепление по порядку величины составит:

                                     DE = W = 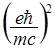/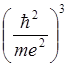.                                      (1.47)

                                          DE = /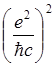.                                                (1.48)

Множитель e²/r есть потенциальная (кулоновская) энергия электрона на орбите и близка по своей величине энергии атома. Второй сомножитель   не имеет размерности и равен 1/137 (постоянная тонкой структуры). Т.о. величина расщепления, связанная со спин-орбитальным взаимодействием в (137)² раз меньше энергии атома. Данный упрощённый расчёт проведён для атома водорода. В общем случае для любого атома расчёты показывают, что величина спин-орбитального взаимодействия сильно возрастает с увеличением заряда ядра (Z⁴).

1.11. Термы состояния атома

          1.11.1. Мультиплетность.

          Рассмотрим систему из двух электронов. Проблема взаимодействия двух электронов является ключевой в квантовой химии, ибо именно взаимодействие двух электронов объясняет природу химической связи.

          В атоме с двумя электронами у каждого  из электронов имеются свои орбитальный и спиновый моменты: l₁, l₂ и s₁, s₂. В s-состоянии l₁ = l₂ = 0, s₁ = s₂ = 1/2. Результирующий МКД будет результатом комбинаций двух спинов:

          m_sz = m_sz^* + m_sz^** = (±1/2) + (±1/2) =  +1, 0, 0, -1.

Значения +1 и -1 получаются, когда спины электронов параллельны, но направлены в разные стороны (­­,¯¯) относительно оси Z и S = 0, когда спины антипараллельны (­¯). Состояние с S = 0 в магнитном поле не расщепляется, а состояние с S = 1 расщепляется на три уровня. Состояния с различными суммарными спинами (S), независимо от числа электронов в системе, называются мультиплетностью и имеют индивидуальные обозначения.