Квантовая химия как наука. Математический аппарат в квантовой химии. Решение волнового уравнения для некоторых частных случаев одномерного движения частицы, страница 6

Рассмотрим линейный самосопряжённый оператор  с дискретными собственными значениями А_nи собственными функциями y_n(x). Любая функция в этом случае может быть представлена в виде ур.1.16. Поскольку функции y_n(x) считаются известными, то для того, чтобы задать j(x), достаточно указать все коэффициенты: с₁, с₂ …, с_n. Следовательно, можно сказать, что полный набор значений с₁, с₂ …, с_n – это и есть функция j(x)  в А–представлении.

Пусть некоторый оператор , действуя на функцию c(x), переводит её в функцию j(x), т.е. имеет место равенство

j(x) = c(x).                                                                         (1.17)

Разложим в ряд функции j(x)  и c(x) по функциям y_n(x):

j(x) =  ;  c(x) =                                                                                                  

и подставим их в ур.1.17. Тогда

 =

или

 =          .                                                        (1.18)

Умножив ур.1.18 на y_k^*(x) и проинтегрировав по всем значениям х, получим следующее равенство:

b_k= .                                                                  (1.19)

Введём обозначение

М_kn =                                                                                     (1.20)

С учётом ур.(1.20) выражение (1.19) принимает вид:

b_k= .

Последнее равенство описывает переход от функции c(x) к функции j(x). Этот переход осуществляется с помощью коэффициентов М_kn. Таким образом, набор всех величин М_kn есть оператор . Совокупность величин М_kn, образующих оператор , записывают в виде матрицы:

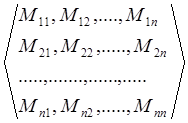      =                                              (1.21)

1.4. Операторы квантовой механики.

1.4.1 Пространственная координата

Координате x соответствует оператор  = x.

1.4.2 Импульс

Составляющей импульса по координате Х – 

p_x ®  = 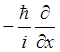,                                                                            (1.22)

а полному импульсу –

 = Ñ.                                                                                        (1.23)

1.4.3 Момент количества движения.

          В классической механике момент количества движения (МКД) – это вектор, который равен произведению вектора-радиуса  на вектор скорости  и на массу m:  = m() =, где   - вектор-импульс (количество движения). Учитывая, что i, j и k – единичные векторы импульсов по координатам X, Y и Z соответственно, и, что i×i =  j×j =  k×k = 0, а i×j =  k, i×k  = -j, j×k = i вычислим произведение .

     = = (xi + yj + zk)( p_xi + p_yj + p_zk) = xp_yk – xp_zj – yp_xk + yp_zi + zp_xj – zp_yi = (yp_z  - zp_y)i + (zp_x – xp_z)j + (xp_y – yp_x)k =   +  + .

По аналогии с классическим моментом количества движения можно написать соответствующие операторы по координатам:

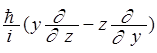           = ;                                                              (1.24)

= ;                     

 = .                       

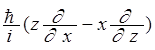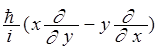В операторах для импульса и момента количества движения появляется мнимая единица (i =). Волновые функции, являющиеся решением уравнения Шредингера, также содержат в себе мнимую единицу. В связи с этим трудно придать физический смысл уравнениям волновой механики, как это было в классической физике.

1.4.4 Оператор спина

          Согласно гипотезе Юленбека и Гаудсмита, электрон, подобно вращающемуся шарику, имеет собственный механический момент, но такой, что его проекция  s_z на любое направление равна половине постоянной планка:

s_z = .                                                                                       (1.25)

Спин сопоставляется с оператором спина  и операторами проекций спина на три оси. Эти операторы между собой не коммутируют.  Коммутаторы операторов спина не равны нулю, а равны , т.е.

            -  =  и т.д.

Спину s_z соответствует магнитный момент

m_z = 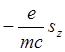.                                                                           (1.26)

          Поэтому кроме оператора  для полного описания свойства спина вводят ещё оператор собственного магнитного момента электрона

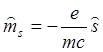          .                                                                             (1.27)

Взаимодействуя с внешним магнитным полем, электрон приобретает энергию

          V_s = .