Проекции промежуточных точек кривой строим либо из условия принадлежности их поверхности конуса (точки 1 и 2 на рис. 16), либо
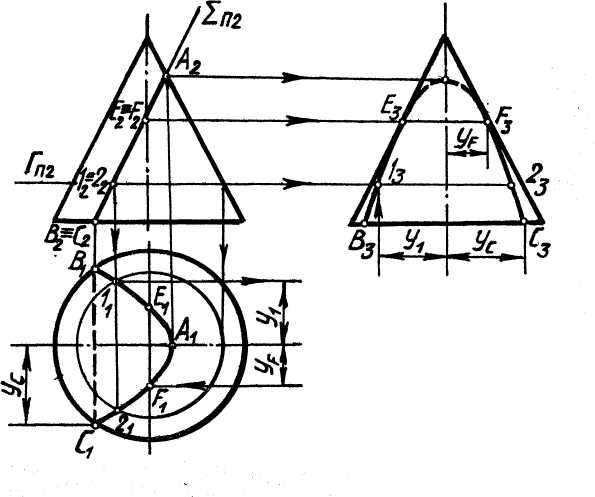 |
одним из известных графических способов. Рассмотрим построение параболы по вершине А и точке С, рис. 17. Порядок построения следующий.
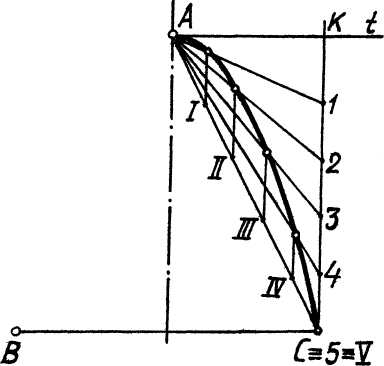 |
Рис.17
Через вершину А проводим прямую t, перпендикулярную оси параболы до пересечения с прямой t в точке К. Соединяем точки А и С. Отрезки АС и КС делим на одинаковое число равных частей и нумеруем их по порядку от точек А и К в направлении к С. Соединяем точку А с точками 1, 2, 3, 4. Через точки I, II, III, IV проводим прямые, параллельные оси параболы. Находим точки параболы как точки пересечения соответственных прямых А - 1 и прямой, проходящей через точку II и т.д.
После определения достаточного количества точек на проекциях параболы, соединяем их плавной лекальной кривой, соблюдая видимость.
Рассмотрим пересечение конуса профильной плоскостью S(SП2), параллельной оси конуса (угол j = 0°), рис. 18.
Поскольку j < y (секущая плоскость параллельна двум образующим конуса, являющимся очерковыми на профильной проекции), то линией пересечения будет гипербола, с вершиной в точке А и точками В и С. Построение проекций гиперболы ясно из чертежа.
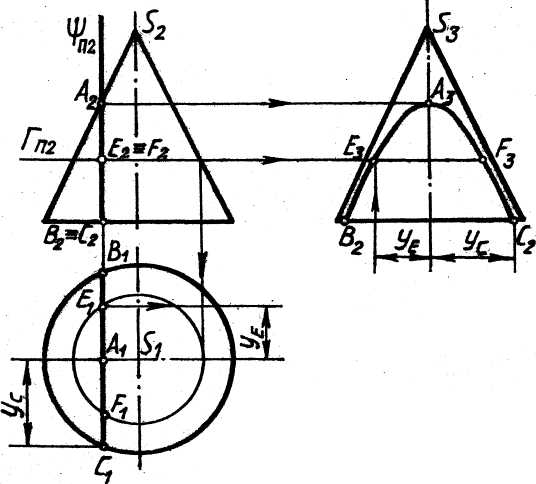 |
Рис.18
2.2.3 Сфера
Плоскость всегда пересекает сферу по окружности. Вид проекций окружности зависит от положения секущей плоскости по отношению к плоскостям проекций:
1) секущая плоскость, параллельная одной из плоскостей проекций,
пересекает сферу по окружности, проецирующейся на эту плоскость без искажения, а на две другие – в отрезки прямых, равные диаметру окружности;
2) секущая плоскость, перпендикулярная одной из плоскостей проекций, пересекает сферу по окружности, проецирующейся на эту плоскость
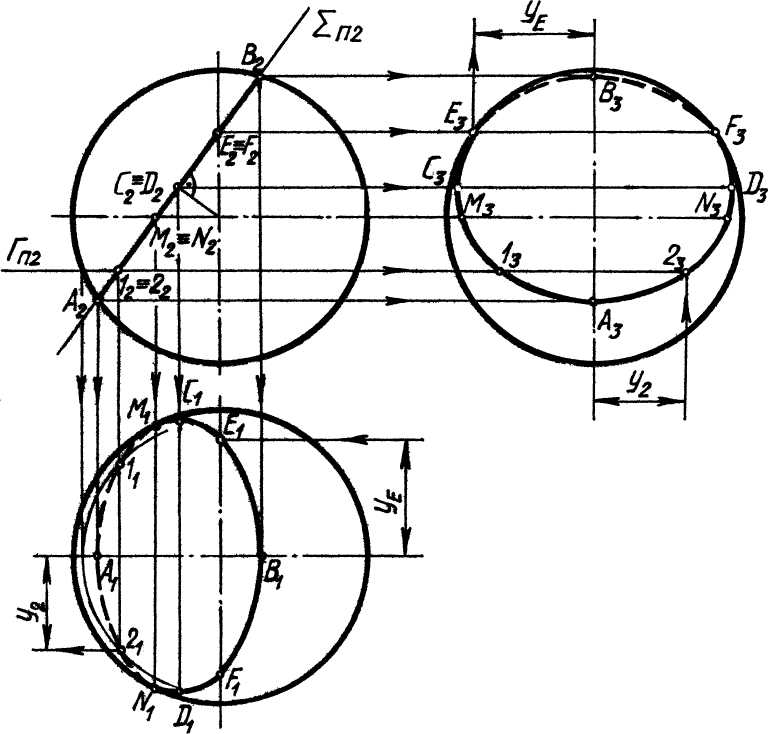 |
Рис.19
отрезком прямой, равным диаметру окружности, а на две другие плоскости – эллипсами;
3) секущая плоскость занимает общее положение. Проекциями окружности на все плоскости проекций будут эллипсы.
Рассмотрим построение проекций линии сечения сферы фронтально-проецирующей плоскостью S (SП2), рис.19. Фронтальная проекция окружности сечения вырождается в отрезок прямой А2В2, равный диаметру окружности. Горизонтальная и профильная проекции будут эллипсами.
Строим характерные точки эллипсов-проекций, то есть концы больших и малых осей. Для этого выделяем два взаимно перпендикулярных диаметра окружности, которые сохранят при проецировании прямой угол и дадут оси эллипса на П1 и П3. Это будут: диаметр CD ^ П2, (C2 º D2 делит пополам отрезок А2В2 или определяется как основание перпендикуляра, опущенного из фронтальной проекции центра шара на А2В2) и диаметр АВ ^ СD. Диаметр CD, как параллельный плоскостям проекций П1 и П3, будет проецироваться на эти плоскости без искажения, т.е. в натуральную величину. Проекции диаметра CD будут большими осями эллипсов. Проекции диаметра АВ будут малыми осями эллипсов.
К характерным точкам эллипсов-проекций относятся также точки касания проекций линии сечения к очерковым образующим поверхностей, в которых кривая делится на видимую и невидимую части. Такими точками на горизонтальной проекции являются точки M1 и N1 (определяющиеся по фронтальным проекциям M2 и N2 на экваторе сферы), а на профильной – точки E3 и F3 (определяющиеся по фронтальным проекциям E2 º F2 как принадлежащие профильному меридиану сферы).
Строим проекции промежуточных точек либо из условий принадлежности их сфере (точки I и 2 на рис.19), либо одним из графических способов построения эллипса по двум осям (см. рис. 12). К промежуточным точкам также относятся точки E1 и F1 на горизонтальной проекции, и M3 и N3 – на профильной проекции сферы.
Полученные точки соединяем плавной лекальной кривой с учётом видимости на проекциях.
3 ПОСТРОЕНИЕ ПРОЕКЦИЙ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТИ ЗАДАННОГО ТЕЛА СКВОЗНЫМ ПРИЗМАТИЧЕСКИМ ОКНОМ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.