Проекции геометрических тел: Методическое пособие для студентов (курсантов), изучающих дисциплины “Начертательная геометрия. Инженерная графика”, “Инженерная графика”, “Инженерная и компьютерная графика”, страница 4

     рис. 13в. Получается разомкнутое сечение с двумя несобственными

    точками:

а) гипербола (S Ë S);

б) две пересекающиеся прямые (S Ì S).

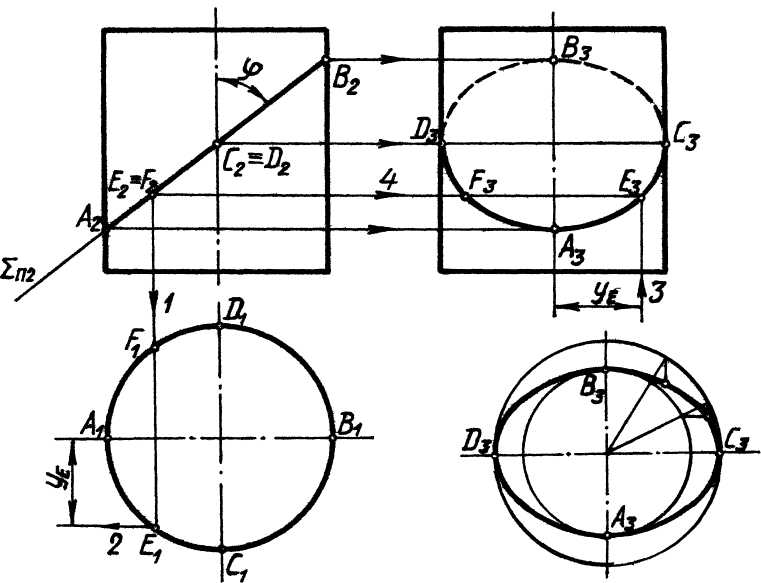                                                               Рис.12

              Рис.13а                             Рис.13б                                  Рис.13в

      На практике, чаще всего, мы имеем дело с конусом – телом, ограниченным одной конической плоскостью и плоскостью основания. В этом случае необходимо помнить, что для определения вида кривой остаются в силе те же признаки. Отличием здесь является лишь то, что характерные точки кривой сечения могут получаться на продолжении конической поверхности (вершина В на рис. 14).

                                                          Рис.14

      Рассмотрим примеры построений проекций линий сечения конуса различными плоскостями. Рассмотрим пересечение конуса фронтально - проецирующей плоскостью S (S_П2), рис. 15. Построение проекций линии сечения осуществляется в следующей последовательности:

1)  определяем вид кривой. т.к. угол   j > y, то линией сечения является

эллипс. Большая ось эллипса АВ равна А₂В₂. Малая ось эллипса CD перпендикулярна П₂ (а значит, параллельна плоскостям П₁ и П₃) и проецируется на фронтальную плоскость проекций П₂                                                в точку (С₂ ≡ D₂)–середину отрезка А₂В₂, а на П₁ и П₃ – в натуральную величину. Проекциями получаемого эллипса, в общем случае, являются эллипсы.

2)  определяем характерные точки проекций эллипса – концы большой и

малой осей эллипсов. Ввиду того, что малая ось эллипса параллельна П₁ и П₃, то по правилу проецирования прямого угла горизонтальные и профильные проекции большой и малой осей эллипса будут также взаимно перпендикулярны, т.е. являются осями эллипсов. Определяем

горизонтальную проекцию А₁В₁ и  профильную проекцию А₃В₃ из условия принадлежности точек А и В очерковым образующим конуса на его фронтальной проекции. Для определения C₁D₁ проводим на конусе через точки C, D вспомогательную окружность в горизонтальной плоскости Г (Г₂). Тогда C₁D₁ находится как хорда проведённой окружности. Координатным способом определяем C₃D₃ (или из условия C₃D₃ = C₁D₁). К характерным точкам профильной проекции эллипса относятся также точки Е₃ и F₃ касания эллипса к очерковым образующим конуса. Точки Е₃ и F₃ разделяют проекцию кривой на видимую и невидимую части и определяются по фронтальной проекции Е₂ ≡ F₂. Проекции Е₁ и F₁ являются промежуточными точками для горизонтальной проекции эллипса. Последовательность их построения отмечена цифрами.

3)  строим промежуточные точки проекций кривой либо из условия

принадлежности их поверхности конуса (по произвольно выбранным фронтальным проекциям точек), либо одним из известных графических способов, рис. 12.

4)  соединяем полученные точки плавной лекальной кривой, соблюдая видимость на проекциях.    

 Рассмотрим построение проекций линий сечения конуса

фронтально– проецирующей плоскостью S(S_П2), рис. 16.

      Плоскость S пересекает конус по параболе, т.к. S параллельна одной образующей конуса (левой очерковой), т.е. j  = y. Характерными точками параболы являются вершина А и точки  В и С.

      Так как ось симметрии, полученной в сечении параболы, является фронталью (парабола симметрична  относительно фронтальной плоскости симметрии конуса), то проекции характерных точек параболы-сечения будут являться также характерными точками парабол-проекций. Проекции А₁ и А₃

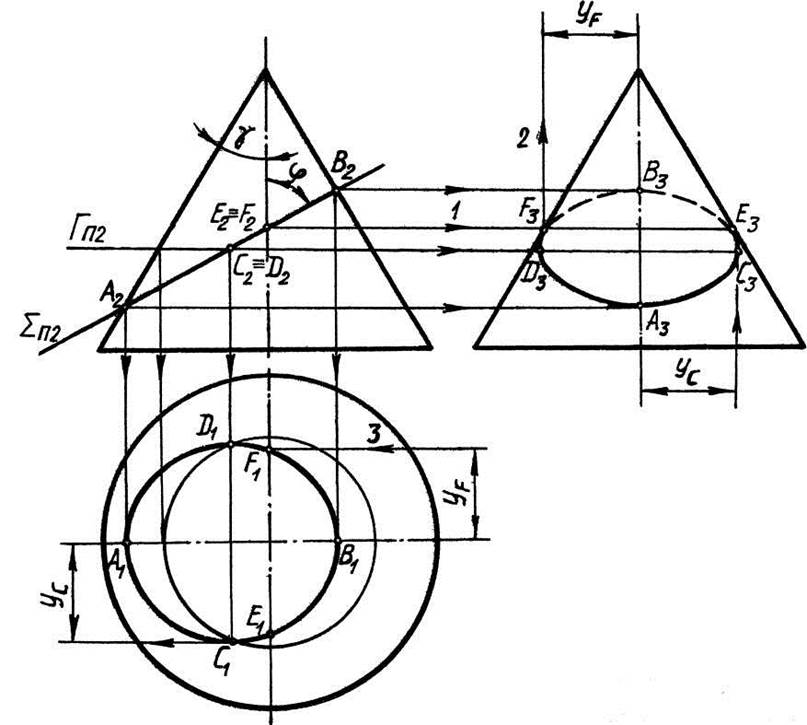
                                                       Рис.15

определены из условия принадлежности точки А правой очерковой образующей   конуса на фронтально проекции. Точки В и С проекций параболы определены из условия их принадлежности окружности основания конуса. К характерным точкам профильной проекции параболы относятся  также точки Е и F касания её к очерковым образующим конуса. Эти точки разделяют проекцию кривой на видимую и невидимую части. Проекции Е₃ и F₃ определяются по фронтальной проекции Е₂ºF₂. Проекции Е₁ и  F₁ являются промежуточными точками на горизонтальной проекции кривой и строятся координатным способом.