Механика \ Начертательная геометрия. Инженерная и машинная графика

Проекции геометрических тел: Методическое пособие для студентов (курсантов), изучающих дисциплины “Начертательная геометрия. Инженерная графика”, “Инженерная графика”, “Инженерная и компьютерная графика”, страница 3

2      ПОСТРОЕНИЕ ПРОЕКЦИЙ ЛИНИИ СЕЧЕНИЯ ЗАДАННОЙ    ПОВЕРХНОСТИ ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ

      Рассмотрим порядок построения линий сечения простейших поверхностей проецирующими плоскостями.

2.1  Поверхности многогранников

      Плоскость пересекает поверхность многогранника по многоугольнику, вершинами которого являются  точки пересечения рёбер многогранника секущей поверхностью.

2.1.2  Прямая призма

     Рассмотрим  построение проекций линии сечения прямой четырёхгранной призмы фронтально-проецирующей плоскостью  S (S П2)   рис. 8. В сечении построен пятиугольник АВСDЕ, у которого вершины В,С и D найдены как точки пересечения плоскости  S с боковыми рёбрами призмы, а вершины А и Е – с рёбрами основания.


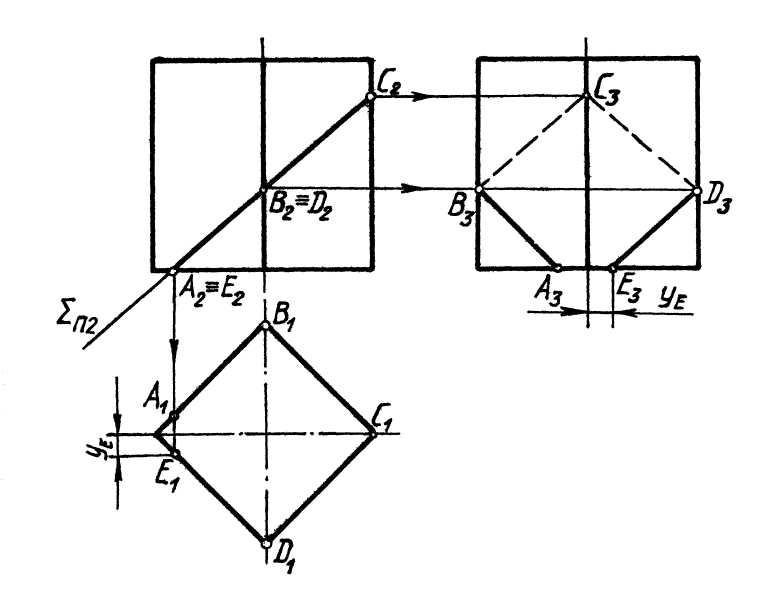                                                        Рис.8

       2.1.2 Прямая пирамида

        Рассмотрим построения проекций линий сечения правильной шестигранной пирамиды фронтально - проецирующей плоскостью S (S П2), рис. 9. В сечении получается шестиугольник АВСКЕD, вершинами которого являются точки пересечения рёбер пирамиды с секущей плоскостью.


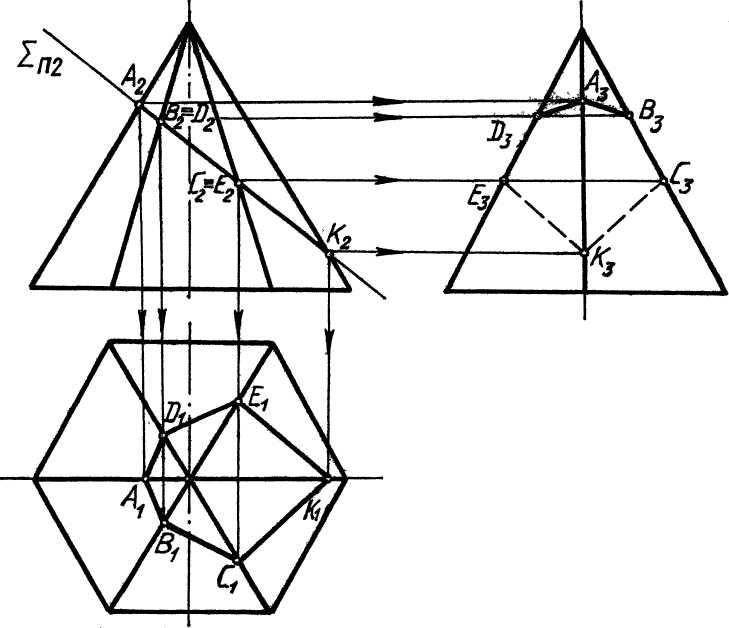                                                           Рис.9   

     Рассмотрим построение проекций выреза пирамиды двумя фронтально- проецирующими плоскостями S (SП2) и Δ (ΔП2), рис.10. Строим шестиугольник АВСКЕD полного сечения пирамиды плоскостью Σ (Σ2). Строим отрезок LM, ограничивающий фигуру сечения (как принадлежащий линии пересечения плоскостей Σ и Δ. Строим фигуру сечения пирамиды плоскостью Δ (ΔП2), ограниченную тем же фронтально-проецирующим отрезком LM.


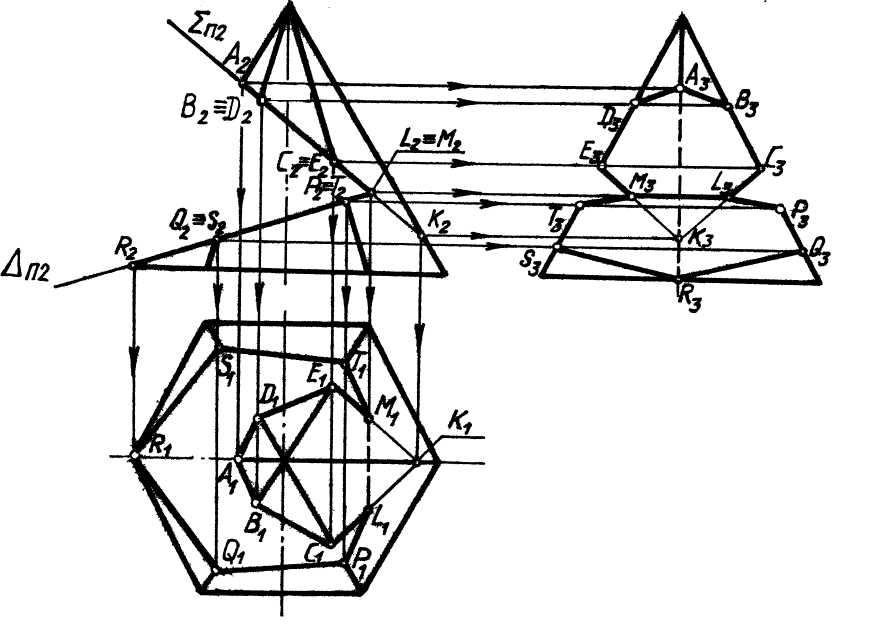
                                                              Рис.10

        2.2  Поверхности вращения

     Линии сечения поверхностей вращения 2-го порядка, ограничивающих заданные тела, в общем случае, являются  кривыми 2-го порядка.

     Для построения проекций искомых линий необходимо:

1)  определить вид получаемой линии;

2)  построить характерные точки для каждой проекции кривой (точки,

определяющие форму проекций кривой и точки касания проекций кривой к очерку поверхности);

3)  построить промежуточные точки проекций кривой;

4)  соединить построенные точки лекальной кривой, соблюдая видимость

 на проекциях.

2.2.1  Прямой круговой цилиндр

      В зависимости от положения секущей плоскости относительно оси (образующих) цилиндра возможны три вида линий сечений:

1)  окружность – секущая плоскость перпендикулярна оси цилиндра;

2)  две параллельные прямые – секущая плоскость параллельна оси

цилиндра, рис. 11;

3)  эллипс – секущая плоскость наклонена к оси цилиндра под углом 0° <


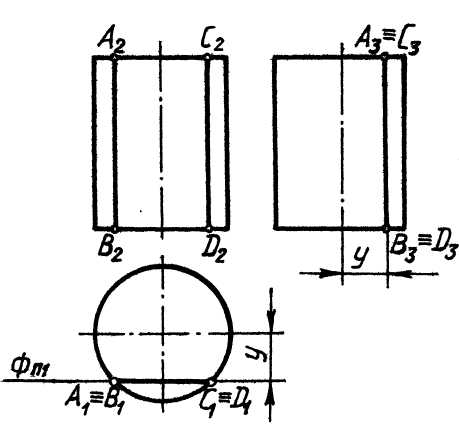j < 90°, рис. 12. Большая ось эллипса  равна отрезку А2В2, а малая – диаметру цилиндра.

                                                        Рис.11

      В зависимости от величины угла j изменяется вид профильной проекции получаемого в сечении эллипса. Так, если j = 45°, то эллипс проецируется в виде окружности. Если j отличен от 45° - в виде эллипса, рис. 12.

      Промежуточные точки профильной проекции строятся либо по их фронтальным проекциям из условия принадлежности точек поверхности цилиндра (точки E и F), либо одним из известных способов построения эллипса по двум осям, рис. 12.

2.2.2  Прямой круговой конус

      Поверхность конуса вращения состоит из двух полостей, симметричных относительно общей вершины S, рис. 13. Обозначим угол наклона секущей плоскости к оси конуса через j, а угол между образующей и осью конуса через y. В зависимости от положения секущей плоскости относительно оси (образующих) конуса в пересечении получаются различные линии:

1.  j > y - секущая плоскость пересекает все образующие конуса в

конечных точках, рис. 13а. Получается замкнутое сечение:

а) эллипс (j ¹ 90°; S Ë S);

б) окружность ( j = 90°; S Ë S);

в) точка (S Ì S);

2.  j  = y - секущая плоскость параллельна одной образующей конуса, т.е.

пересекает её в бесконечно удалённой точке, рис. 13б.  

а) парабола (S Ë S);

б) две совпавшие прямые (S Ì S).

3.  j < y, в частности j  = 0, - секущая плоскость параллельна двум

     образующим конуса, т.е. пересекает их в бесконечно удалённых точках,

Скачать файл