Радиоавтоматика: Методические указания к самостоятельной аудиторной работе, страница 9

При анализе устойчивости и качества переходного процесса в системах автоматического управления не всегда требуется использо­вать аппарат критериев устойчивости или вычислять параметры пере­ходного процесса. Бывают такие ситуации, когда, обладая опреде­ленным опытом или навыками, можно и без сложных вычислений быст­ро ответить на эти вопросы, по крайней мере, в первом приближе­нии. Например, иногда можно без всяких вычислений сказать, что система устойчива (или неустойчива), посмотрев на ее годограф Найквиста, который и является амплитудно-фазовой частотной харак­теристикой разомкнутой системы. Естественно, для этого необходимо хорошо представлять себе годографы всех типовых структурных зве­ньев, а при их последовательном соединении – правило построения суммарного годографа. В табл. 4.1 приведены передаточные функции и годографы наиболее часто встречающихся типовых структурных звеньев.

№ п/п	Наименование звена	Передаточная функция	Вид годографа
1	Инерционное		K
2	Интегрирующее
3	Дифференцирующее идеальное
4	Дифференцирующее реальное		1
5	Упругое дифференцирующее

№ п/п	Наименование звена	Передаточная функция	Вид годографа
6	Упругое интегрирующее
7	Форсирующее		K
8	Колебательное		K

Рассмотрим цепочку из n структурных звеньев (рис.4.1)

 

Рис.4.1

Передаточная функция всей цепи

Соответственно, в частотной области

или, переходя к модулю и фазе

Как известно, модуль произведения комплексных чисел равен произведению модулей сомножителей, а фаза – сумме фаз, т.е.

Пользуясь этими простыми правилами и зная форму годографов каж­дого эвена, можно, по крайней мере, качественно, быстро зарисо­вать форму годографа цепочки последовательно включенных звеньев. Рассмотрим несколько примеров.

Пример I. Имеется 3 последовательно включенных звена: 2 интегрирующих и одно инерционное.

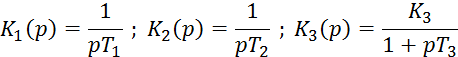
Зарисуем годографы каждого из них:

                                                                                                                     K₃

Пока нет навыка зарисовки суммарного годографа, можно посмотреть модуль и фазу комплексного коэффициента передачи каждого звена на нулевой и на бесконечной частотах, а также динамику их изме­нения при возрастании частоты, а затем сложить фазовые сдвиги и перемножить модули коэффициентов передачи. Конкретно, для данно­го примера:

Перемножая модули, получаем:

                 

Складывая фазы, получаем:

              

                 

Следовательно, годограф группы звеньев начинается на низких частотах в бесконечности под углом – (-180), т.е. слева по вещественной оси, а заканчивается на очень высоких частотах в начале координат, подходя к нему сверху (-270). В промежутке между  и  все три звена имеют плавное снижение модулей усиления, а фазовый сдвиг у первых двух звеньев неизменен (по - 90), а у инерционного звена плавно нарастает от 0 до -90.

С учетом всего сказанного выше, возможна лишь одна форма годографа данной группы звеньев (рис.4.2)

                                                                 Im

 

                                                    -1                                       Re

 

Рис.4.2

Если предположить, что эта группа звеньев охвачена отрица­тельной обратной связью, т.е. представляет собой замкнутую авто­матическую систему, то, пользуясь критерием Найквиста, можно сказать, что эта система неустойчива. Особенностью ее является то, что она будет неустойчива при любых коэффициенте усиления  и постоянных времени , так как годограф всегда про­ходит выше точки (-1). Изменяя , , можно изменить лишь форму и масштабы кривой, но все равно годограф будет располагаться в верхнем левом квадранте и охватывать точку (-1). Такие и подобные им системы, неустойчивые при любых значениях параметров входящих в них звеньев, называют структурно неустойчивыми.   Это именно тот случай, когда одного взгляда на структуру системы и тем более на ее годограф достаточно для заключения об устойчивос­ти, и нет никакой необходимости проводить численный анализ по критериям устойчивости.