Радиоавтоматика: Методические указания к самостоятельной аудиторной работе, страница 8

   (3.2)

Если это условие не выполняется, дальнейший анализ можно не про­водить – система неустойчива. Если же условие (3.2) выполняется, то проверяется достаточное условие – положительность всех диаго­нальных определителей матрицы Гурвица. Эта матрица составляется из коэффициентов уравнения (3.1) по очень простым правилам:

I) матрица содержит h строк и n столбцов;

2) по главной диагонали с верхнего левого угла до нижнего правого вписываются коэффициенты от  до ;

3) остальные места можно заполнять так: по строке вправо вписываются коэффициенты с возрастанием индекса, влево – с убыванием. Можно то же самое делать по столбцам: вверх – с убывающим индексом, вниз – с возрастающим. Результат будет один и тот же. Например, для системы с дифференциальным уравнением 5-го порядка характеристическое уравнение будет иметь вид

А матрица Гурвица выглядит следующим образом:

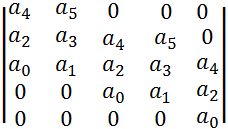
Достаточные условия устойчивости - положительные значения всех диагональных определителей:

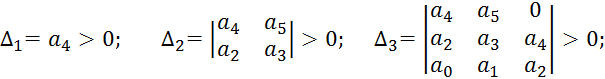
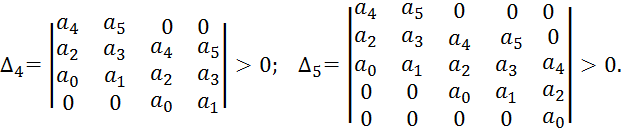
В результате для уравнения 5-й степени условия Гурвица сводятся к двум неравенствам:

Аналогичные условия можно получить и для других порядков:

                                

Для более низких порядков n достаточно проверки только положительности коэффициентов характеристического уравнения.

Рассмотрим два примера.

Пример I. Система следящая, состоит из одного интегрирующего и двух инерционных звеньев

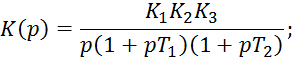
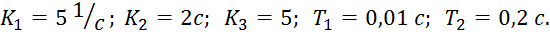
Получим характеристический полином замкнутой системы , являющийся, как известно, знаменателем передаточной функции замкнутой системы Ф(p). Для следящих систем

что дает для данного примера:

Обозначим коэффициенты характеристического полинома:

Запишем условие Гурвица для системы 3-го порядка

или, после подстановки коэффициентов

Это есть условие устойчивости. Если неравенство превратить в равенство, возникает так называемое критическое состояние системы, когда она находится на грани между устойчивым и неустойчивым сос­тояниями. Коэффициент усиления при этом называют критическим

Полученное выражение показывает, что в рассмотренной системе (одно интегрирующее звено и два инерционных) можно добиться больших значения   путем уменьшения постоянных времени инерционных звеньев. А теперь подставим численные значения

С другой стороны

Таким образом, при заданных параметрах рассматриваемая система неустойчива, так как ее коэффициент усиления  больше критического  . Систему можно сделать устойчивой, либо уменьшив усиление примерно в 5 раз, либо уменьшив одну или обе постоянные времени .

Пример 2.  Система из трех инерционных звеньев (рис.3.1)

 

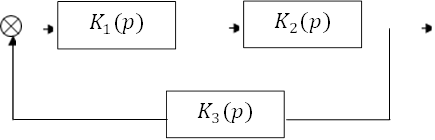Рис.3.1

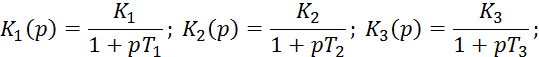
Для структуры рис.3.1.

Отсюда характеристический полином

где

Подставив коэффициенты в условие Гурвица для уравнений третьей степени, для критического коэффициента усиления получаем

откуда

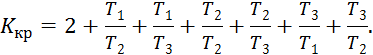
Из этого следует, что в данной системе критический коэффициент усиления зависит не от абсолютных значений постоянных времени, а только от их отношений. Например, если бы те же числа постоянных времени были в размерности не секунды, а милли- или микросекунды, то с точки зрения устойчивости ничего бы не изменилось.

Подсчитаем  для данных значений параметров системы

Заданный коэффициент усиления

Следовательно, система по примеру 2 устойчива, так как е коэффициент усиления меньше критического (примерно в 3 раза).

Задачи для самостоятельного решения в аудитории

Задача 3.I. Следящая система со структурой:

Проанализировать по критерию Гурвица.

Задача 3.2. Следящая система со структурой:

Задача 3.2. В примере по задаче 3.2 сменить коэффициент усиления , увеличив его в 10 раз, затем в 100. Сделайте выводы по данной задаче.

Задача 3.4. Следящая система со структурой:

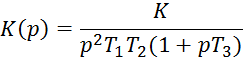
Проанализировать по критерию Гурвица.

Задача 3.2. В примере по задаче 3.4 уменьшить коэффициент усиления в 10 раз, в 1000 раз. Исследовать устойчивость, сделать выводы по структурной схеме задачи 3.4.

Тема 4. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЦЕПОЧКИ ТИПОВЫХ СТРУКТУРНЫХ ЗВЕНЬЕВ

Цель занятия. Научиться зарисовывать вид амплитудно-фазовых частотных характеристик (годографов), последовательно соединен­ных типовых структурных звеньев.