Радиоавтоматика: Методические указания к самостоятельной аудиторной работе, страница 6

                                                       …………………………

или, опуская промежуточные функции

откуда эквивалентная передаточная функция последовательной цепоч­ки звеньев

т.е. при последовательном включении звеньев эквивалентная переда­точная функция равна их произведению.

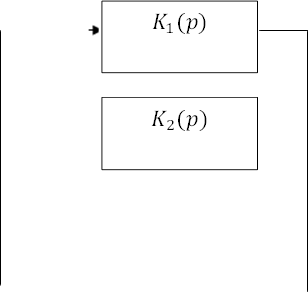
Так же просто можно получить результат на примере параллель­ного включения звеньев (рис.2.3).

Поскольку структурный анализ основан на принципе однонаправ­ленности звеньев, т.е. считается, что передаточная функция звена не зависит от сопротивления нагрузки, можно предполагать, что ре­зультаты прохождения сигнала   через каждое звено  линейно складываются на общей нагрузкеявляющейся входным сопротивлением остальной части системы.

Тогда  

Где – эквивалентная передаточная функция группы параллельно включенных звеньев.

 

                                                                               

 

                                                                                                    

 

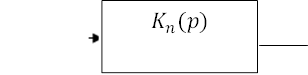Рис.2.3

Рассмотрим теперь случаи встречно-параллельного включения (рис.2.4). Здесь кроме двух звеньев обязательно присутствует сумматор, замыкающий обратную связь, причем сумматор вычитающий. Такая обратная связь называется отрицательной.

Эквивалентная передаточная функция такого соединения будет отношением изображения по Лапласу выходного сигнала к входному.

                                                                     (2.1)

Выразим ее через передаточные функции звеньев и .

Запишем очевидные отношения

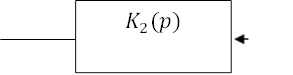Рис.2.4

Исключим отсюда  и  как не входящие в формулу (2.1)

                                                       (2.2)

                                            (2.3)

Подставляя (2.2) и (2.3) в уравнение сумматора, получаем

Разделяя переменные, получаем

Это и есть эквивалентная передаточная функция встречно-параллельного включения звеньев.

Весьма полезными при структурных преобразованиях оказываются также правила переноса точки приложения воздействия на систему и точки съема сигнала системы. Рассмотрим конфигурацию фрагмента структуры системы рис.2.5.

                 

 

   

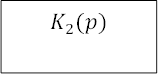Рис.2.5

Здесь на систему подается управляющий и дополнительный сигнал  (это может быть, например, возмущающий сигнал). Допустим, по какой-то причине необходимо сместить точку приложения сигнала , например, перенести ее на вход звена . Чтобы результат воздействия на систему не изменился, при этом между воздействием  и новой точкой приложения необходимо включить звено с передаточной функцией . Тогда схема будет выглядеть как на рис.2.6.

                 

 

 

 

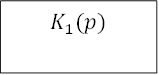
Рис.2.6

Точно так же точку приложения воздействия можно переносить с выхода звена (группы звеньев) на вход, но при этом воздействие необходимо сначала пропустить через звено с обратной передаточной функцией (рис.2.7).

 

                                                                

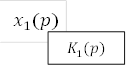Рис.2.7

Подобные правила существуют и для переноса точки съема сигнала с системы.

 

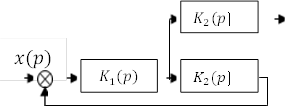
Рис.2.8

 

Рис.2.9

Иллюстрации рис. 2.8, 2.9 можно охарактеризовать правилом: при пе­реносе точки съема сигнала с выхода звена (группы звеньев) на его вход (против направления распространения информации) необходимо добавлять звено с передаточной функцией этого звена (группы звень­ев). Перенос точки съема сигнала по ходу распространения информа­ции требует включения звена с обратной передаточной функцией. Те­перь, используя вышеизложенные правила, можно произвести структур­ные преобразования схемы рис.2.1.

Прежде всего заменим соединения звеньев и ,  и  их соответствующими эквивалентами: