Радиоавтоматика: Методические указания к самостоятельной аудиторной работе, страница 11

Цель занятия. Изучить один из способов анализа устойчивости линейных автоматических систем, научиться решать задачи устойчи­вости конкретных автоматических систем методом чередующихся кор­ней.

Метод чередующихся корней - это, по существу, приложение или следствие к критерию устойчивости Михайлова. Он позволяет, во всяком случае, для систем с характеристическими уравнениями до 5 порядка включительно, быстро произвести анализ устойчивости по критерию Михайлова без построения годографа Михайлова.

Как известно, по Михайлову система n -го порядка будет ус­тойчива, если годограф характеристической частотной функции в диапазоне частот от 0 до   последовательно против часовой стрелки обходит n квадратов комплексной плоскости (рис.5.1).

                                                           Im

                                                                                 n=5

 

                                                                                                     Re

 

                                                                          

                                         n=3                                  n=4

Рис.5.1

Из рис. 5.1 видно, что если система устойчива, то годограф функции ζ( поочередно пересекает вещественную и мнимую оси и не может подряд два раза пересечь одну и ту же ось. Именно проверка этого обстоятельства и составляет сущность метода чередующихся корней. Обратим внимание, в частности, на годограф при n=5, осей  - вещественной оси,  ,  - мнимой оси. Если вычислить значение всех этих частот и расставить их в ряд по порядку возрастания численных значений, то при устойчивой системе не могут оказаться рядом два числа с четными (пересечение вещественной оси) или с нечетными индексами (пересечение мнимой оси).

Рассмотрим два примера.

Пример I. Пусть имеется система со структурой:

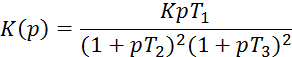
Характеристический полином данной системы

или после преобразований

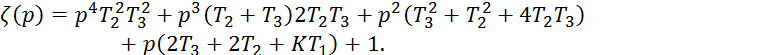
Переходим в частотную область

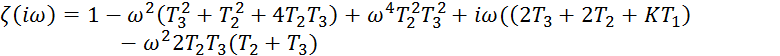
обозначим и вычислим коэффициенты:

Найдем частоты пересечения мнимой оси, для чего приравняем к нулю вещественную часть и найдем корни полученного уравнения.

Заменим переменную

Взяв только положительные значения частот, получаем:

 

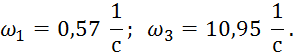
Находим частоты пересечения вещественной оси:

откуда

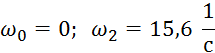
Расположим все четыре частоты пересечения осей по порядку их возрастания и подчеркнем корни одного уравнения сплошной чертой, а другого – волнистой:

0 ,               0.57,            10.95,          15.6

Как видим, рядом расположены два корня одного уравнения  , значит два раза подряд с ростом частоты пересекается мнимая ось. Система неустойчива. Теперь, исключительно ради интереса, можно нарисовать примерную форму годографа данной системы 4-го порядка

                                                                Im

 

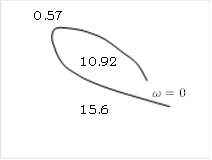                                                                                            Re

 

Условие Михайлова не выполняется.

Пример 2. В системе по примеру I изменим величину коэффициента усиления. Вместо K=200 возьмем K=25. Вычислим и запишем новые коэффициенты характеристического уравнения:

Повторим решение уравнений Re

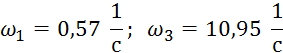
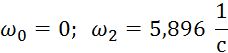
Выписываем частоты в ряд, как прежде:

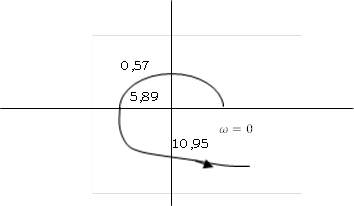
0 ,               0.57,            5.896,          10.95

Корни чередуются. Правило чередующихся корней выполняется, следовательно, система устойчива. Можно нарисовать, как выглядит годограф Михайлова

 

    Im

                                                                                              Re

Задачи для самостоятельного решения в аудитории

Задача 5.I. Задана структура системы:

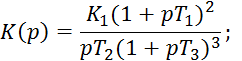
Исследовать устойчивость методом чередующихся корней. Нарисовать как выглядит годограф Михайлова.

Задача 5.2. Повторить решение по предыдущей структуре с параметрами:

Задача 5.3. Задана структура системы:

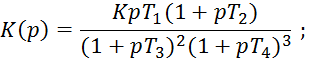
Исследовать устойчивость методом чередующихся корней. Нарисовать как выглядит годограф Михайлова.