Радиоавтоматика: Методические указания к самостоятельной аудиторной работе, страница 5

Тема 2. СТРУКТУРНЫЕ СХЕМЫ И СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ

Цель занятия: Усвоить назначение структурных схем, основные правила преобразования структурных схем. Научиться решать задачи  сведения разветвленной структурной схемы к простейшему виду и оп­ределять сигналы в различных точках системы при известном входном сигнале.

Одним из важнейших этапов исследования автоматической системы  является составление ее структурной схемы, позволяющей в последую­щем выйти на уровень математического описания процессов, протекаю­щих в системе. Принципиальное отлитие структурных схем от функци­ональных состоит в том, что если последние позволяют рассмотреть систему на уровне принципа ее работы и связей между основными эле­ментами, то структурная схема каждому функциональному элементу (например: детектор, смеситель, усилитель, генератор и т.п.) ста­вит в соответствие его математическое описание, т.е. оператор. Математическое описание элемента структурной схемы в принципе   может быть различным: дифференциальное уравнение; импульсная характерис­тика; переходная характеристика; комплексный коэффициент передачи; передаточная функция; матрица сопротивлений (проводимостей) и дру­гие. Однако в теории автоматического управления в подавляющем боль­шинстве случаев в качестве математического описания структурного звена используют передаточную функцию (оператор Лапласа). Нельзя сказать, что это традиция или так сложилось исторически. Дело в том, что большинство практически существующих автоматических сис­тем имеют довольно сложные, часто разветвленные структуры, с не­сколькими петлями обратной связи. Вместе с тем, анализ процессов в системах, расчет их рабочих характеристик требуют упрощения сложных структур, сведения их к простейшим (например, к одной или двум эквивалентным структурным единицам, охваченным обратной свя­зью). Такая работа связана с преобразованием сложных структурных схем, когда последовательно сворачиваются к эквивалентным струк­турным единицам целые группы звеньев, часто вместе с местными пет­лями обратных связей. В процессе преобразований структурных схем наиболее удобным и быстрым является использование именно оператор­ного метода, когда в качестве математического описания структурного звена выступает передаточная функция. При этом выигрыш в трудо­емкости по сравнению с другими способами математического описания структурных звеньев настолько большой, что операторный метод сегодня является основным в теории автоматического управления, осо­бенно при преобразованиях структурных схем. Рассмотрим учебный пример структурной схемы и произведем ее преобразования к простей­шему виду. Пусть исходная (непреобразованная) структурная схема выглядит так, как показано на рис.2.1.

                                                                                                   4

Рис.2.1

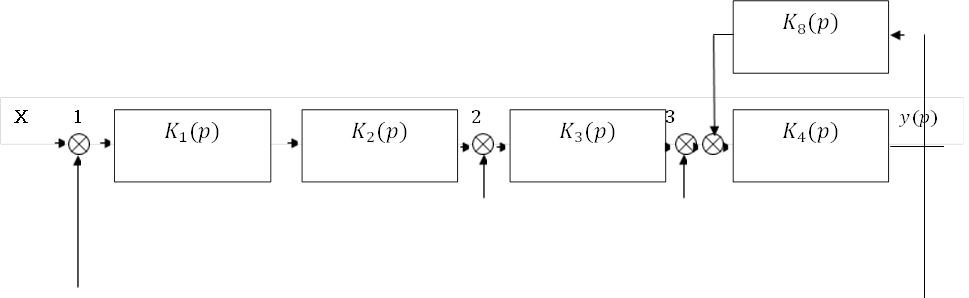
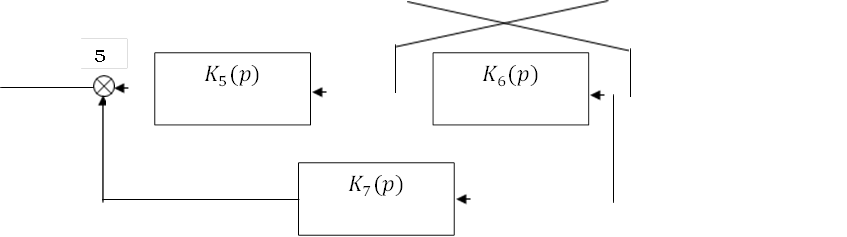
На схеме рис.2.1 имеются 8 структурных звеньев, заданных свои­ми передаточными функциями и 5 сумматоров, обозначенных, как при­нято в автоматике, кружочком, разделенным на 4 сектора. У любого сумматора один выход и до 3 входов, причем сигнал с входа, под­ключенного к не заштрихованному сектору сумматора, передается на выход без изменений, а сигнал с входа - к заштрихованному секто­ру, передается на выход с инверсией полярности (т.е. вычитается). Например, для сумматора I справедливо уравнение

так как сигнал Z(p)подается на инверсный вход сумматора. По существу, такой сумматор является вичитателем, то же самое относи к сумматорам 2,3,4. А сумматор 5 действительно суммирует оба сиг­нала, которые на него подаются, так как у него не заштрихован ни один сектор.

Присмотревшись к схеме рис.2.1, можно заметить некоторые ти­повые структуры:

-  последовательное включение звеньев (например, звеньев  и );

- параллельное включение звеньев (например, звеньев  ,  и );

- встречно-параллельное включение звеньев (например, звенья  и   через сумматор 4).

Каждую из таких типовых структур можно заменить одним звеном с некоторой эквивалентной передаточной функцией. Например, пусть имеется цепочка последовательно включенных звеньев (рис.2.2).

Рис.2.2

Очевидно, что

                                                       …………………………