Дальнейшему упрощению схемы мешает наличие перекрещивающихся связей с входа и выхода звена 6 на сумматоры 2,3. Необходимо от этого избавиться. Проще всего это можно сделать, перенося точку съема сигнала с выхода звена C на его вход. С учетом этого и упрощений в звеньях 1,2 и 4,8 структурная схема может быть зарисована несколько иначе (рис.2.10).
Теперь
можно продолжить преобразование структурной схемы. В частности, звенья ![]() и
и ![]() вместе с
сумматором 3 можно заменить эквивалентом встречно-параллельного включения.
вместе с
сумматором 3 можно заменить эквивалентом встречно-параллельного включения.
![]()
Звенья 5 и 6 включены последовательно, а параллельно с ними включено звено 7. Их общая передаточная функция
![]()
![]()
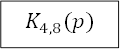
![]()
![]()
![]()
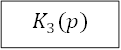
![]()
![]()
![]()
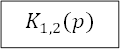 x1
𝜉 2 3 y
x1
𝜉 2 3 y
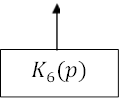 |
|||||||||||
![]()
![]() z
z
![]()
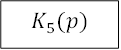
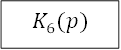 4
4
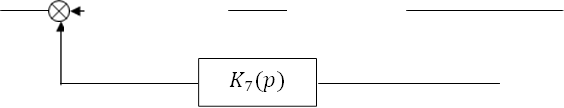 |
Рис.2.10
С учетом этих преобразований схема принимает вид
![]()
![]()
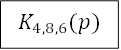
![]()
![]()
![]()
![]()
![]()
![]()
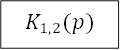
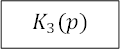
![]() x 𝜉 y
x 𝜉 y
![]()
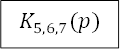
![]() z
z
Дальнейшее
преобразование связано с свертыванием звеньев ![]() ,
, ![]() и сумматора 2
и сумматора 2
![]()
после чего
полученное эквивалентное звено оказывается включенным последовательно с звеном ![]() . Обозначим эквивалент последовательного соединения
звеньев
. Обозначим эквивалент последовательного соединения
звеньев ![]() и
и ![]() через
через ![]() ,
, ![]() .
.
![]()
![]()
Тогда окончательно схема примет вид
![]()
![]()
![]()
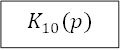
![]()
![]()
![]()
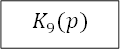
![]() x 𝜉 y
x 𝜉 y
![]() z
z
Что является, по существу, обычным встречно-параллельным включением, рассмотренным ранее. Теперь, считая сигнал x заданным, мы можем найти сигналы y,z,𝜉с помощью операторного метода
![]()
![]()
![]()
На этом рассмотрение примера можно закончить.
Задачи для самостоятельного решения
Задача 2.I. Задана структура системы
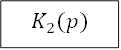
![]()
![]()
![]()
![]()
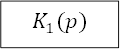 x 𝜉 y
x 𝜉 y
 |
|||||||||
![]()
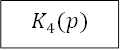
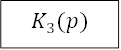 z
z
 |
|||
Задано изображение входного сигнала x(p). Произвести упрощение схемы и определить изображение сигналов y(p),z(p),𝜉(p).
Задача 2.2. Задана структура системы
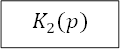 |
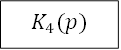
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
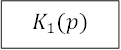
![]()
![]() x 𝜉 y
x 𝜉 y
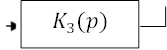 |
|||||||||
![]() z
z
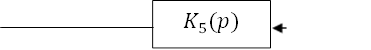 |
Упростить структурную схему и определить сигналы y(p),𝜉(p),z(p), если x(p) задано.
Тема 3. АЛГЕБРАИЧЕСКИЙ КРИТЕРИЙ УСТОЙЧИВОСТИ ГУРВИЦА
Цель занятия. Изучить самостоятельно критерий устойчивости Гурвица, научиться исследовать по этому критерию автоматические системы произвольной структуры.
Еще в конце восьмидесятых годов XIX века выдающийся русский математики и механик А.М.Ляпунов сформулировал известные теоремы устойчивости. Исследование устойчивости по А.Н.Ляпунову сводится к доказательству отсутствия в характеристическом полиноме системы корней с положительными или нулевыми вещественными частями. Однако пользоваться таким способом анализа устойчивости не всегда удобно, так как это связано с необходимостью отыскания корней алгебраического уравнения типа
![]() (3.1)
(3.1)
где n – целое положительное число.
Поэтому многими специалистами в области математики, механики и автоматики велись поиски условий, выполнение которых гарантировало бы отрицательные значения вещественной части всех корней характеристического уравнения. Такие условия устойчивости получили название критериев устойчивости. Первыми появились алгебраические критерии устойчивости, затем, уже в 30-х годах XX века – частотные. Среди алгебраических критериев наиболее известный и удобный для практического применения – критерии Гурвица (1895 г.). Гурвиц доказал, что если наложить определенные условия на коэффициенты уравнения (3.1), то при их выполнении все корни данного уравнения будут иметь отрицательные вещественные части. Эти условия можно разделить на необходимые и достаточные. Необходимым условием устойчивости является положительность всех коэффициентов уравнения (3.1):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.