МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
"ХАРЬКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ"
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторной работе № 7 "Дискретное преобразование Фурье"
по курсу "Обработка сигналов и изображений"
для студентов специальностей 7.091501, 7.091502, 7.091503 дневной формы обучения
ХАРЬКОВ НТУ "ХПИ" 2006
1. ЦЕЛЬ ЛАБОРАТОРНЫХ ЗАНЯТИЙ
Получение практических навыков в преобразовании входных цифровых сигналов с временной в частотную область, реализованных в пакете MatLab.
2. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
Непрерывные преобразования
Фурье требуют больших вычислительных затрат при их осуществлении.
Кроме того, в век цифровых технологий непрерывные сигналы
повсеместно вытесняются дискретными и цифровыми сигналами. Поэтому
основой практической реализации спектрального анализа Фурье является алгоритм дискретного
преобразования Фурье - ДПФ. Полученная совокупность ![]() оцифрованных
выборок косинусоидального
оцифрованных
выборок косинусоидального ![]() и синусоидального
и синусоидального ![]() преобразования подаются на устройство,
осуществляющее дискретное преобразование в соответствии с соотношением:
преобразования подаются на устройство,
осуществляющее дискретное преобразование в соответствии с соотношением:
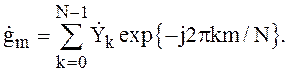 (1)
(1)
Здесь
![]() спектральная плотность напряжения
спектральная плотность напряжения ![]() той гармоники последовательности
той гармоники последовательности ![]()
Найденная совокупность комплексных чисел ![]() представляет собой дискретную выборку
спектральной плотности напряжения огибающей колебаний
представляет собой дискретную выборку
спектральной плотности напряжения огибающей колебаний ![]() .
Далее полученная спектральная плотность перемножается с частотной
характеристикой фильтра. Ее значение представляет преобразование Фурье от
импульсной характеристики. Результат перемножения в виде совокупности комплексных
чисел
.
Далее полученная спектральная плотность перемножается с частотной
характеристикой фильтра. Ее значение представляет преобразование Фурье от
импульсной характеристики. Результат перемножения в виде совокупности комплексных
чисел ![]() представляет спектральную плотность
напряжения на выходе фильтра. Для получения временной структуры выходного
сигнала необходимо осуществить обратное преобразование Фурье вида:
представляет спектральную плотность
напряжения на выходе фильтра. Для получения временной структуры выходного
сигнала необходимо осуществить обратное преобразование Фурье вида:
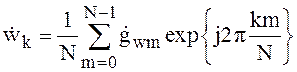 . (2)
. (2)
Остановимся на физической трактовке рассматриваемого
преобразования. При ![]() выражение имеет вид:
выражение имеет вид:
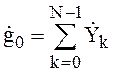 .
(3)
.
(3)
Так как экспоненциальный множитель (1) при ![]() равен единице при всех значениях
равен единице при всех значениях ![]() , выражение (3) представляет собой с
точностью до константы среднее значение всех
, выражение (3) представляет собой с
точностью до константы среднее значение всех ![]() выборок
выборок
![]() Это значение определяет амплитуду гармоники
нулевой частоты спектральной плотности
Это значение определяет амплитуду гармоники
нулевой частоты спектральной плотности ![]() .
Соответственно при
.
Соответственно при ![]() выражение для ДПФ имеет вид:
выражение для ДПФ имеет вид:
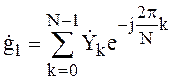 .
(4)
.
(4)
Значение ![]() означает амплитуду
первой гармоники найденного дискретного преобразования. Заметим, что
представленное преобразование позволяет оценить амплитуды
означает амплитуду
первой гармоники найденного дискретного преобразования. Заметим, что
представленное преобразование позволяет оценить амплитуды ![]() гармоник, начиная с нулевой и до
гармоник, начиная с нулевой и до ![]() ой. Действительно, задавая
ой. Действительно, задавая ![]() , легко убедиться, что в силу периодичности
экспоненциальной функции
, легко убедиться, что в силу периодичности
экспоненциальной функции ![]()
![]() . Иначе для значений
. Иначе для значений ![]() полученные значения
полученные значения ![]() повторяются.
повторяются.
Остановимся на физической сущности найденных значений ![]() и ее связи с реальной спектральной
плотностью напряжения. Для этого проанализируем экспоненциальный множитель
и ее связи с реальной спектральной
плотностью напряжения. Для этого проанализируем экспоненциальный множитель ![]() . Умножим числитель и знаменатель
показателя степени на интервал дискретизации
. Умножим числитель и знаменатель
показателя степени на интервал дискретизации ![]() .
Показатель степени представим в виде:
.
Показатель степени представим в виде: 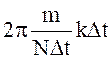 . Знаменатель
. Знаменатель ![]() представляет
время наблюдения
представляет
время наблюдения ![]() принимаемой реализации,
принимаемой реализации, ![]() текущее дискретное время. В этом случае
значение
текущее дискретное время. В этом случае
значение ![]() может быть записано в виде
может быть записано в виде
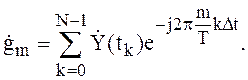 (5)
(5)
При этом значение частоты ![]() той
гармоники равна
той
гармоники равна ![]() Герц. Конкретные значения частот
гармоник и их количество, полученное путем ДПФ, рассмотрим на простом примере.
Допустим время наблюдения равно
Герц. Конкретные значения частот
гармоник и их количество, полученное путем ДПФ, рассмотрим на простом примере.
Допустим время наблюдения равно ![]() мкс, интервал дискретизации
мкс, интервал дискретизации
![]() мкс. Тогда количество выборок
мкс. Тогда количество выборок ![]() . Частота
. Частота ![]() той
гармоники реального сигнала равна
той
гармоники реального сигнала равна ![]() кГц. Последняя гармоника
частоты 1,9 МГц. Спектральные линии отстоят друг от друга по оси частот с интервалом
100 кГц.
кГц. Последняя гармоника
частоты 1,9 МГц. Спектральные линии отстоят друг от друга по оси частот с интервалом
100 кГц.
Таким образом, дискретное преобразование Фурье совокупности ![]() дискретных выборок наблюдаемой реализации
дискретных выборок наблюдаемой реализации ![]() позволяет оценить
позволяет оценить ![]() дискретных
значений спектральной плотности напряжения
дискретных
значений спектральной плотности напряжения ![]() ,
равномерно расположенных в диапазоне частот от нуля до
,
равномерно расположенных в диапазоне частот от нуля до ![]() (
(![]() частота дискретизации) с интервалом
частота дискретизации) с интервалом ![]() . Полученная спектральная плотность
напряжения повторяется с периодом
. Полученная спектральная плотность
напряжения повторяется с периодом ![]() .
.
Вычисление ДПФ по ранее приведенному соотношению (4) требует
весьма большого числа операций: примерно ![]() операций
умножения и
операций
умножения и ![]() операций сложения. При большом значении
операций сложения. При большом значении ![]() такой алгоритм потребует большего бюджета
времени для решения задачи фильтрации и последующего обнаружения сигнала и
оценки его параметров.
такой алгоритм потребует большего бюджета
времени для решения задачи фильтрации и последующего обнаружения сигнала и
оценки его параметров.
Количество операций умножения (самых продолжительных в вычислительных устройствах) окажется даже для самой простой задачи большим. Поэтому необходим поиск способов, позволяющих сохранять преимущество цифровой обработки в частотной области по сравнению с временной, и требующих меньших временных затрат. В настоящее время разработан ряд алгоритмов вычисления ДПФ при значительном сокращении бюджета времени, называемые алгоритмами быстрого преобразования Фурье (БПФ).
Остановимся на одном из алгоритмов БПФ, обеспечивающем
выигрыш по операции умножения в ![]() раз по сравнению с
ДПФ. Такой выигрыш достигается в случае, когда величина
раз по сравнению с
ДПФ. Такой выигрыш достигается в случае, когда величина ![]() выбирается
кратной
выбирается
кратной ![]() . Здесь
. Здесь ![]() – целое
число. Приведенное ранее выражение для ДПФ (4) представим в виде:
– целое
число. Приведенное ранее выражение для ДПФ (4) представим в виде:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.