Дискретное преобразование Фурье: Методические указания к лабораторной работе № 7 по курсу "Обработка сигналов и изображений", страница 3

	1				1				(16)
		1
			1
				1				–
	1				–1		–1
		1				–
			1				–
				1				–

Во всех пустых клетках этих матриц должны быть записаны нули. Можно убедиться, что их произведение дает матрицу . Разложение матриц на “простые сомножители” вида (13) называют факторизацией.

Процедуру вычисления дискретного спектра удобно представить в виде графа, приведенного на рис. 2. Граф поясняет последовательность действий, предписываемых факторизованной матрицей.

Если дискретизация во времени производилась с шагом , то последовательность  описывает частотный спектр через интервал , где  – полная длительность сигнала. Весь спектр при этом занимает область частот от 0 до .

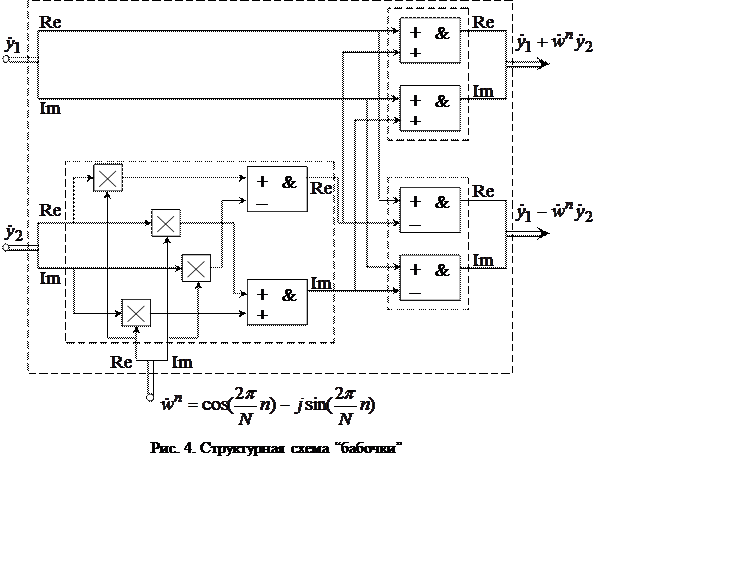
В настоящее время широко используются интегральные микросхемы, выполняющие четырех точечное БПФ, являющееся базовой операцией. Эту микросхему называют “бабочкой”, она позволяет формировать спецпроцессоры БПФ для сигналов с произвольным .

Функциональная схема “бабочки” и ее условные обозначения показаны на рис. 3. Если на ее выход поступают комплексные числа  и , то на выходе формируются два числа  и . Поскольку комплексные величины представляют собой пару чисел (реальные и мнимые части), то практически “бабочка” имеет четыре входа и четыре выхода (рис. 4).

На рис. 5 приведена схема восьми точечного спецпроцессора БПФ, реализованного с помощью “бабочки”. Нетрудно убедиться, что в схеме осуществляются операции, предписанные факторизованной матрицей (13).

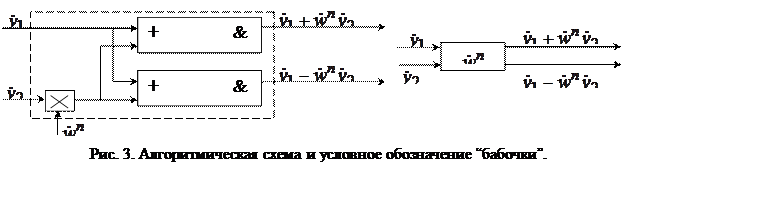
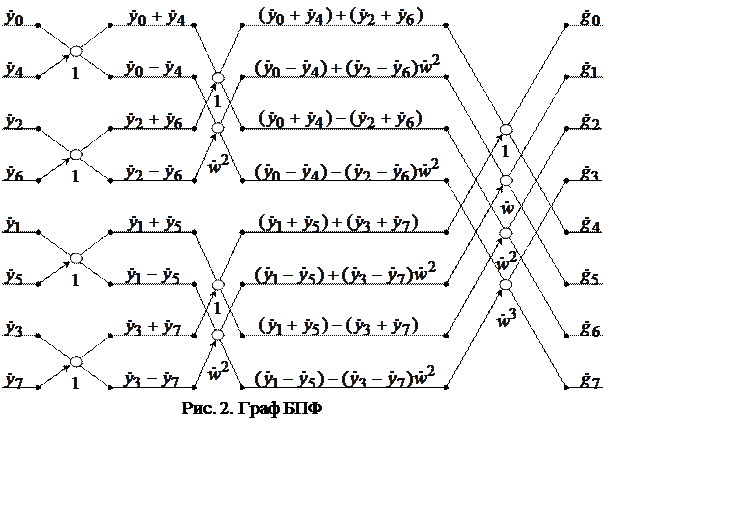Формально БПФ осуществляется путем разбиения исходной последовательности на четные (, , ,…) и нечетные (, , ,…) последовательности. С ними поступают аналогичным образом. Эти процедуры повторяются до тех пор, пока не останется по одной паре чисел, которые поступают на “бабочки” первого этапа. Применительно к восьми точечному БПФ этими парами являются , , , . На первом этапе операции умножения практически не производятся (умножение на ). Здесь формируются суммы и разности пар.

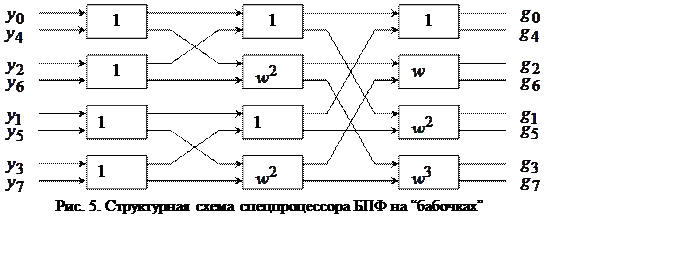
Далее алгоритм вычисления ясен из рис. 5. Видно, что вся операция состоит из трех этапов. В общем случае для – точечного БПФ (обычно ) нужно  этапов. На каждом из них выполняется  операций умножения. Таким образом, алгоритм БПФ содержит всего  операций умножения. Поэтому БПФ по сравнению с ДПФ дает выигрыш по операциям умножения в  раз.

В заключение отметим, что при реализации цифровой обработки в частотной области необходимо соблюдать условия неискаженной фильтрации. Последнее может возникнуть при неправильном выборе числа дискретных значений, подвергаемых дискретному преобразованию Фурье сигналов. Ранее было указано, что при выборе числа временных дискрет, равном , неповторяющаяся совокупность спектральных составляющих ДПФ также равна  и наоборот. Поэтому минимальное значение , обеспечивающее неискаженную обработку сигналов, должно выбираться из условия

.

Здесь  – количество ненулевых дискретных значений наблюдаемой реализации ,  – количество ненулевых дискретных значений полезного сигнала. Такой выбор  позволяет решать задачи обнаружения и измерения координат наблюдаемых объектов при произвольном временном запаздывании полезного сигнала в пределах длительности наблюдаемой реализации .

3. ДИСКРЕТНЫЕ БЫСТРЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ

В ПАКЕТЕ MATLAB