Основой практической реализации спектрального анализа Фурье является алгоритм быстрого дискретного преобразования Фурье — БПФ. Он реализован особым пирамидальным алгоритмом, и в нем используется процедура прореживания по частоте. Это исключает многочисленные повторы в вычислениях функций синуса и косинуса и устраняет избыточность спектров.
Алгоритм БПФ, в пакете Matlab, реализован функцией
Y = fft(Х,n).
Функция Y = fft(Х) вычисляет для массива данных Х дискретное преобразование Фурье, используя FFT-aлгоритм быстрого Фурье-преобразования. Если массив X двумерный, вычисляется дискретное преобразование каждого столбца.
Функция Y = fft(X, n) вычисляет n точечное дискретное преобразование Фурье. Если length(X) < n, то недостающие строки массива X заполняются нулями: если length(X) > n то лишние строки удаляются.
Основное назначение преобразования Фурье - выделить частоты регулярных составляющих сигнала, зашумленного помехами. С ее помощью по известному вектору сигнала х(k) вычисляется вектор:
,
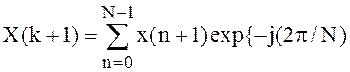где N=lengh (Х) — длина вектора исходных данных. Если N есть степень числа 2, то используется высокоэффективный алгоритм БПФ для вещественных или комплексных данных. Время вычислений для комплексных данных примерно на 40—50 % больше, чем для действительных. Если N является простым числом, выполняется алгоритм дискретного преобразования Фурье — ДПФ — по приведенной выше формуле. Если N < nто недостающие элементы массивах дополняются нулями.
Прямое БПФ переводит представление сигнала из временной области в частотную область. Проиллюстрирует это, для чего рассмотрим следующий пример:
Пусть входной дискретный сигнал поступает с частотой 1000 Гц. Сформируем сигнал, содержащий регулярные составляющие с частотами 50 и 130 Гц с случайную аддитивную компоненту с нулевым средним
t = 0:0.001:1; % Вектор времени
х = sin (2*pi*50*t) +sin (2*pi*130*t); % Вектор входного сигнала
y=x+2*randn(size(t));% Сумма сигнала и помехи
plot(y(1:50)),grid
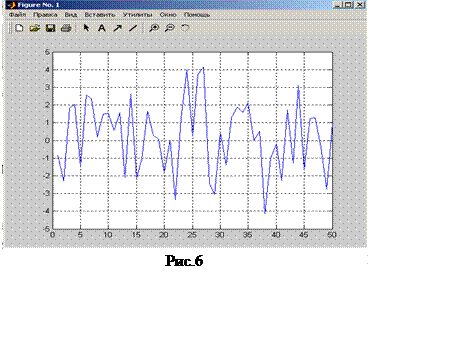На рис.6
показан этот сигнал. Глядя на него трудно сказать, каковы частоты его
регулярных составляющих. Реализуя одномерное преобразование Фурье этого сигнала
на основе 512 точек и построив график спектральной плотности (рис.7), можно
выделить две частоты, на которых амплитуда спектра максимальна. Это частоты 130
Гц и 50 Гц.
Y=fft(x,512); % Вектор ДПФ сигнала
F=Y.*conj(Y)/512;
f=1000*(0:255)/512;
figure(2),plot(f,F(1:256)),grid
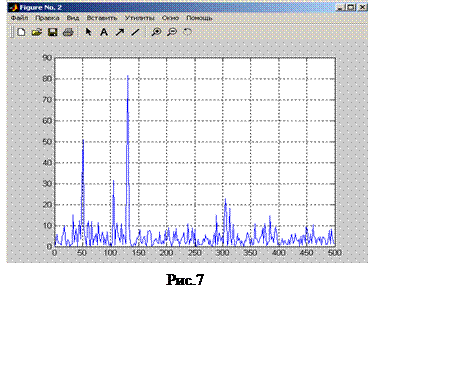Результаты расчета
частотных составляющих входного сигнала представлены на рис.7.
Этот пример показывает задание вектора временной зависимости сигнала, представленного суммой двух синусоид с частотами 50 и 130 Гц и аддитивной помехой. При необходимости отобразить АЧС и ФЧС поступают следующим образом. Исключают помеху и производят следующие вычисления:
m = abs(Y); p = unwrap(angle(Y));% Векторы амплитуд и фаз
f=1000*(0:255)/512;% Вектор частот
figure(2),plot(f,m(1:256)),grid %Графики AЧХ
 |
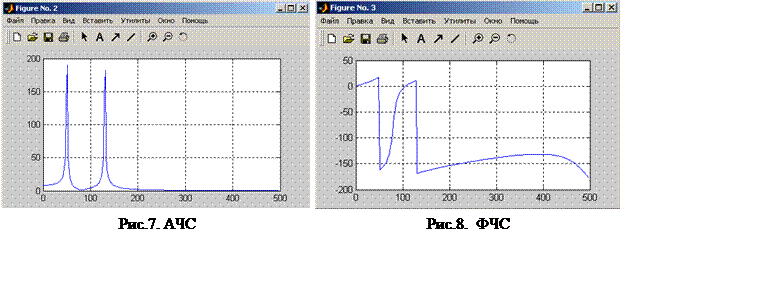Результаты расчета представлены на рис. 7 (АЧХ) и 8 (ФЧХ).
При
выполнении прямого БПФ спектральные компоненты, близкие к нулевой частоте, группируются
по краям спектрограммы, например, рис. 7. Функция
у = fftshift(x)
обеспечивает перегруппировку элементов выходного массива преобразования Фурье таким образом, что эти компоненты оказываются в центре графика, т.е. перегруппировывает выходные массивы функций fft и fft2, размещая нулевую частоту в центре спектра.
Это иллюстрирует следующий пример:
Y=fftschift(fft(x,512)); % Вектор ДПФ сигнала
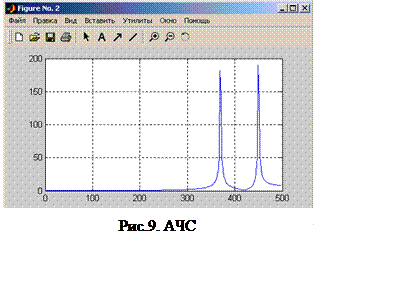
Рис.9 показывает АЧС исследуемого колебания для этого примера. Сравнив рис. 9 с рис. 7 нетрудно заметить, что нулевая частота здесь соответствует центру графика.
Все сказанное об алгоритме БПФ относится и к обратному преобразованию, которое реализуется функцией у = ifft (х [, n]). Для проверки функций fft и ifft можно использовать следующий пример:
» х=[1 2 3 4];
>> X=fft(x)
X =
10.0000 -2.0000+2.0000i -2.0000 -2.0000-2.0000i
>> x=ifft(X)
1 2 3 4
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.