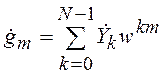Дискретное преобразование Фурье: Методические указания к лабораторной работе № 7 по курсу "Обработка сигналов и изображений", страница 2

,                                                         (6)

где .

Пользуясь матричной символикой, представим (6) в виде:

,                                               (7)

где  и  – матрицы-столбцы (векторы) принимаемой реализации и спектра, а  – матрица ДПФ. Обычно следует размерности векторов выбирать одинаковыми, тогда  – квадратная матрица.

Проанализируем подробно операции ДПФ на примере  (в силу ряда причин следует стремиться к тому, чтобы  было равно целой степени числа 2). Итак, для рассматриваемого случая

.                                                   (8)

Матрица ДПФ, в соответствии с (8), принимает вид (9).

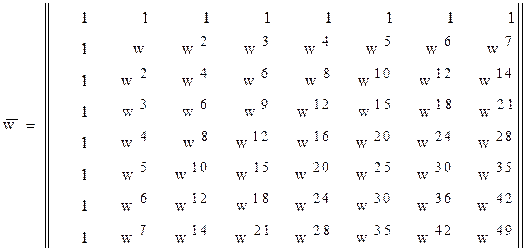
.                                (9)

Обратимся к анализу величины . На рис. 1 представлена комплексная плоскость, на которой изображена окружность единичного радиуса. Точки  находится на этой окружности, и представляют собой периодическую последовательность. Все , лежащие в пределах от 0 до 7, полностью определяют любую степень при . Суммы вида (6) называют свертками. Свертки, обладающие описанным свойством, называют круговыми. Обратим внимание на то, что числа, соответствующие точкам, расположенным на противоположных концах диаметра, отличаются лишь знаком. Следовательно: ; ; ; . Иначе, любая целая степень  может быть выражена через  , ,  (конечно, ). С учетом сказанного матрицу ДПФ представим в виде

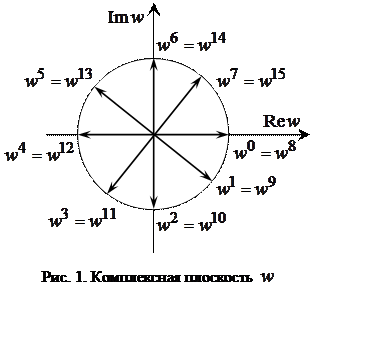
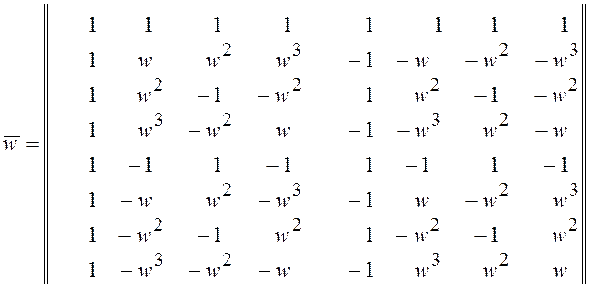.                   (10)

Проанализируем полученную матрицу. В каждой ее строке встречаются либо одинаковые, либо отличающиеся знаками члены. Идея БПФ использует описанные выше свойства круговой свертки и, кроме того, предусматривает сокращение операций умножения в соответствии с тождеством

.                                       (11)

Слева в этом равенстве две операции умножения, справа – одна. С учетом этих замечаний найдем составляющие дискретного спектра

Видно, что в круглых скобках содержатся линейные комбинации элементов вектора . Таких комбинаций восемь. В квадратных скобках комбинации круглых скобок (их тоже восемь). Наконец, последние операции предусматривают создание весовых сумм из квадратных скобок.

Эти последовательные операции могут быть представлены в виде произведения трех сравнительно простых матриц (соответственно справа налево). Таким образом, матрица ДПФ принимает вид

,                                                            (13)