Дискретное преобразование Фурье: Методические указания к лабораторной работе № 7 по курсу "Обработка сигналов и изображений", страница 6

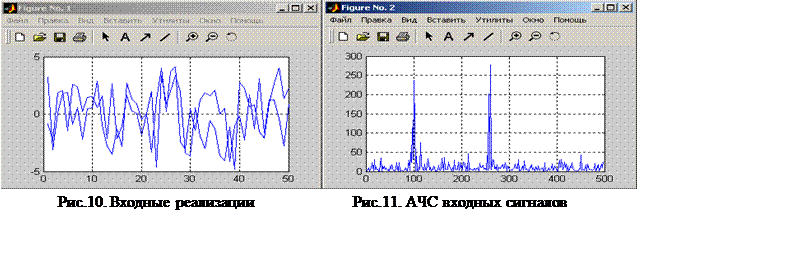
Применим двумерное преобразование Фурье для сигнала у на основе 512 точек и построим график спектральной плотности. Теперь можно вы­делить 2 частоты, на которых амплитуда спектра максимальна (рисю11). Это часто­ты - 100/2Гц и 240/2Гц.

Y= fft2(y, 2, 512);
Pyy = Y.*conj(Y)/512;
f= 1000*(0:255)/512;
figure(2>, plot(f, Pyy(1:256)), grid

Двумерное дискретное преобразование связано с одномерным дискрет­ным преобразованием Фурье следующим образом: fft2(X) = fft(fft(X).').'

3. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

1.  Ознакомьтесь с краткими сведениями из теории дискретного преобразования Фурье.

2.  Создайте журнал выполнения лабораторной работы.

3.  Сформируйте сигнал

,

где  (N – Ваш номер по журналу) содержащий регулярную составляющую с частотой . Частота поступления данных равна 1000 Гц. Постройте график сформированного сигнала.

4.  Реализуйте одномерное преобразование Фурье этого сигнала на основе 512 точечного преобразования и постройте график спектральной плотности.

5.  Реализуйте одномерное преобразование Фурье этого сигнала на основе 128 точечного преобразования и постройте график спектральной плотности.

6.  Проведите сравнительный анализ результатов, полученных в п.4 и 5.

7.  Сформируйте принимаемое колебание,

в составе сигнала, содержащий регулярные составляющие с частотами ,  и случайной аддитивной компоненты с нулевым средним. Частоту поступления (F) данных и параметры входных колебаний выбрать в соответствии с Вашим вариантом, который определяется Вашим номером в журнале (если Ваш номер (N) больше 17, номер варианта равен N-17). Постройте график сформированного сигнала.

Таблица 1

8.  Реализуйте одномерное преобразование Фурье этого сигнала на основе 512 и 256 точечного преобразования, постройте графики спектральных плотностей и проведите сравнительный анализ полученных результатов.

9.  Сформируйте две входных последовательности на примере рассматриваемого сигнала и постройте графики. Примените двумерное преобразование Фурье для рассматриваемого сигнала на основе 512 точек и постройте график спектральной плотности. Сделайте выводы.

10. Сформируйте вектор строку из 10 случайных чисел. Выполните прямое ДПФ. Отобразите результаты в отчете. Выполните обратно ДПФ над полученными значениями. Отобразите результаты в отчете. Сделайте выводы.

11. Оформите отчет по лабораторной работе.

1.  СПИСОК ЛИТЕРАТУРЫ

1.  Дьяконов В.П. MATLAB 6.5 SP1/7.0 Simulink 5/6/ - М.: СОЛОН-Пресс, 2005. – 575 с.

2.  Потемкин В.Г. MATLAB. – М.: Диалог.- 1997. -341 с.