Міністерство освіти та науки України
Національний технічний університет “ХПІ”
Кафедра обчислювальної техніки та програмування
ЗВІТ
про виконання лабораторної роботи №7
з навчальної дисципліни “ Обробка сигналів”.
Виконав:
Студент гр. КІТ-14 б
Богачов О. С.
Викладач:
Філатова Г.Є.
Федюшин О.І..
Харків 2008
Тема: Дискретне перетворення Фур'є.
Мета: Отримання практичних навиків в перетворенні вхідних цифрових сигналів з тимчасовою в частотну область, реалізованих в пакеті MatLab.
Індивідуальне завдання:
|
№ варианта |
F |
|
|
|
|
|
|
5 |
500 |
60 |
90 |
2 |
2 |
2 |
Хід роботи
Сформуємо сигнал ![]() , де f1=10*N (N=5).
, де f1=10*N (N=5).
>>t = 0:0.001:1;
>>х = sin (2*pi*50*t);
>>y=x+2*randn(size(t));
>>plot(y(1:50)),grid
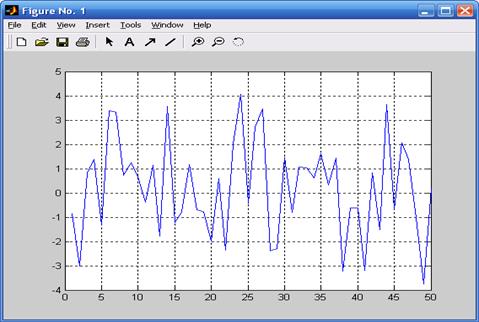
Реалізуємо одномірне перетворення Фур’є цього сигналу на основі 512 крапкового перетворення та будуємо графік спектральної щільності.
>>t = 0:0.001:1;
>>x = sin (2*pi*50*t);
>>y=x+2*randn(size(t));
>>plot(y(1:50)),grid
>>Y=fft(x,512);
>>F=Y.*conj(Y)/512;
>>f=1000*(0:255)/512;
>>figure(2),plot(f,F(1:256)),grid
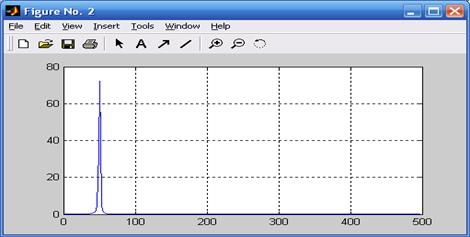
Реалізуємо одномірне перетворення Фур’є цього сигналу на основі 256 крапкового перетворення та будуємо графік спектральної цільності.
>>t = 0:0.001:1;
>>x = sin (2*pi*50*t);
>>y=x+2*randn(size(t));
>>plot(y(1:50)),grid
>>Y=fft(x,128);
>>F=Y.*conj(Y)/128;
>>f=1000*(0:255)/128;
>>figure(2),plot(f,F(1:128)),grid
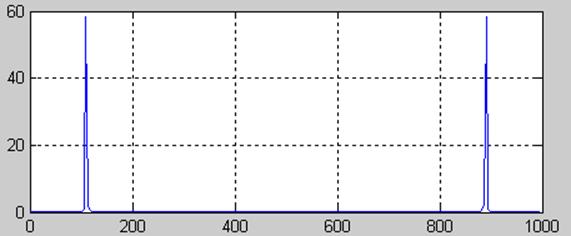
Сформувати прийняте коливання, х=k1sin(2Пf1t)+k2sin(2Пf2t) у складі сигналу, що містить регулярні складові із частотами f1, f2.
![]()
>> t=0:0.001:1
>> x=1*sin(2*pi*70*t)+1*sin(2*pi*80*t)+3;
>> plot(x(1:50)),grid
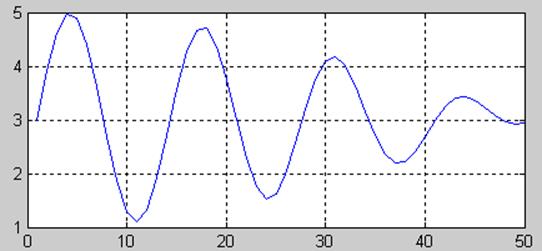
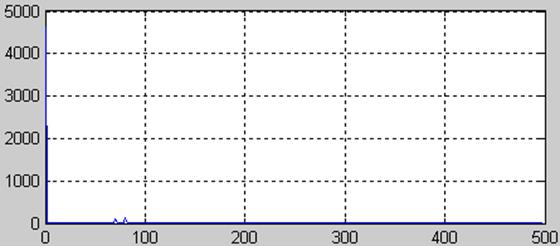
Реалізуємо одномірне перетворення Фур'є цього сигналу на основі 512 і 256 крапкового перетворення, побудуємо графіки спектральних цільностей і проведемо порівняльний аналіз отриманих результатів.
>>t = 0:0.001:1;
>>x=1*sin(2*pi*70*t)+1*sin(2*pi*80*t)+3;
>>Y=fft(x,512);
>>F=Y.*conj(Y)/512;
>>f=1000*(0:255)/512;
>>figure(2),plot(f,F(1:256)),grid
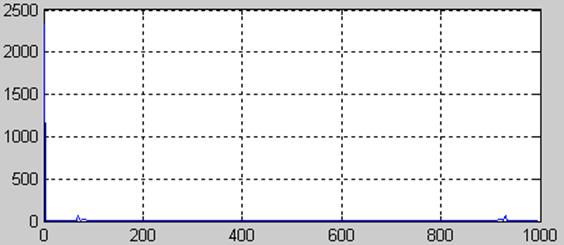
>>t = 0:0.001:1;
>>x=1*sin(2*pi*70*t)+1*sin(2*pi*80*t)+3;
>>Y=fft(x,256);
>>F=Y.*conj(Y)/256;
>>f=1000*(0:255)/256;
>>figure(2),plot(f,F(1:256)),grid
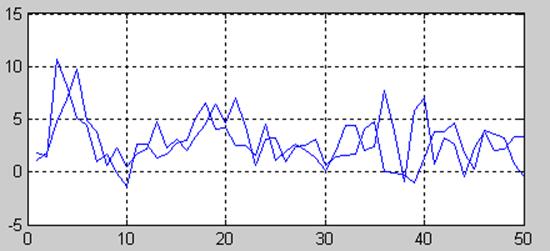
Сформуємо 2 вхідних послідовності на прикладі розглянутого сигналу й побудувати графіки. Застосувати двовимірне перетворення Фур'є для розглянутого сигналу на основі 512 крапок і побудувати графік спектральної щільності. Зробити висновки.
>>x=1*sin(2*pi*70*t)+1*sin(2*pi*80*t)+3;
>>y1=x+2*randn(size(t));
>>y2=x+2*randn(size(t));
>>y=[y1;y2];
>>plot(y(1,1:50)),hold on, plot(y(2,1:50)), grid, hold off
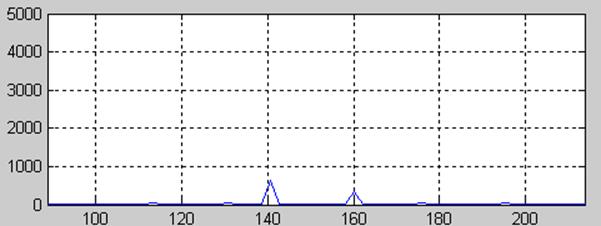
>>Y= fft2(y, 2, 512);
>>Pyy = Y.*conj(Y)/512;
>>f= 1000*(0:255)/512;
>>figure(2), plot(f, Pyy(1:512)), grid
>>figure(2), plot(f, Pyy(1:256)), grid
Сформувати вектор-рядок з 10 випадкових чисел. Виконати пряме ДПФ. Відобразити результати у звіті. Виконати зворотне ДПФ над отриманими значеннями. Відобразити результати у звіті. Зробити висновки.
>> x=[1,2,3,4,3,1,5,2,1,2]
x =
1 2 3 4 3 1 5 2 1 2
>> X=fft(x)
X =
24.0000 -3.8541 - 2.6287i -2.3820 - 1.9021i 2.8541 + 4.2533i -4.6180 - 1.1756i 2.0000
-4.6180 + 1.1756i 2.8541 - 4.2533i -2.3820 + 1.9021i -3.8541 + 2.6287i
>> x=ifft(X)
x =
1 2 3 4 3 1 5 2 1 2
Виконавши пряме та зворотне ДПФ початковий вектор було відновлено.
Висновок: в ході лабораторної роботи отримали практичні навички у перетворенні вхідних цифрових сигналів з тимчасовий у частотну область, реалізованих у пакеті MatLab.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.