МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
„ХАРЬКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ”
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к лабораторной работе
"Исследование время-частотных характеристик сигналов"
по курсу "Обработка сигналов и изображений"
для студентов специальностей 7.091501, 7.091502, 7.091503
дневной формы обучения
ХАРЬКОВ НТУ "ХПИ" 2006
1. ЦЕЛЬ ЛАБОРАТОРНЫХ ЗАНЯТИЙ
Получение практических навыков расчета время-частотных характеристик сигналов, используемых в информационных системах.
2.КРАТКИЕ СВЕДЕНИЯ С ТЕОРИИ
В информационных системах используются:
- прострой (узкополосный) сигнал без внутриимпульсной модуляции;
- линейно-частотно-модулированный (ЛЧМ) сигнал;
- фазокодоманипульрованный (ФМ) сигнал.
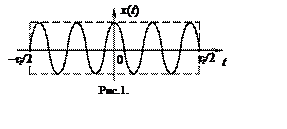 Узкополосный
сигнал без внутриимпульсной модуляции
образуется за счет импульсной модуляции, при которой колебание излучается в
пространство не непрерывно, а дискретно в виде коротких импульсов. Время
излучения характеризуется длительностью импульса
Узкополосный
сигнал без внутриимпульсной модуляции
образуется за счет импульсной модуляции, при которой колебание излучается в
пространство не непрерывно, а дискретно в виде коротких импульсов. Время
излучения характеризуется длительностью импульса ![]() , а
интервал времени между импульсами называется периодом следования (повторения)
(Т).
, а
интервал времени между импульсами называется периодом следования (повторения)
(Т).
Примером такого сигнала показан на рис.1.
Под узкополосными понимают радиоимпульсы, для которых выполняется условие
![]() . (1)
. (1)
Безразмерная величина B в (1) называется коэффициентом широкополосности или базой сигнала.
Для рассматриваемого радиоимпульса комплексная огибающая сигнала является действительной функцией
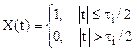 (2)
(2)
имеющей частотный спектр
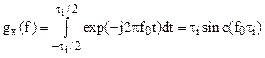 .
(3)
.
(3)
Здесь
и далее функция ![]() .
.
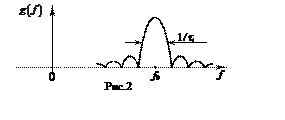 Амплитудно-частотный
спектр (АЧС) такого сигнала показан на рис.2.
Амплитудно-частотный
спектр (АЧС) такого сигнала показан на рис.2.
При обработке такого
сигнала стараются исключить частоту несущего колебания (![]() ),
т.е. перейти к видеосигналу, вид и АЧС которого приведен на рис.3.
),
т.е. перейти к видеосигналу, вид и АЧС которого приведен на рис.3.
Линейно-частотно модулированные сигналы образуются при частотной модуляции, когда принудительному изменению подлежит мгновенная частота СВЧ колебания. В настоящее время широкое распространение получили сигналы с линейной частотной модуляцией (ЛЧМ сигналы), когда мгновенная частота зондирующего сигнала изменяется по линейному закону. Одновременное использование частотной и импульсной модуляций обеспечивает формирование зондирующих ЛЧМ радиоимпульсов.
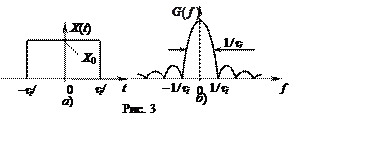 ЛЧМ
радиоимпульс (рис.4,а) описывается выражением
ЛЧМ
радиоимпульс (рис.4,а) описывается выражением
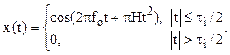 (4)
(4)
Мгновенная частота импульса определяется дифференцированием полной фазы
![]() ,
(5)
,
(5)
где
![]()
Видно, что f(t)
изменяется по линейному закону (рис.4,б). В пределах импульса частота
изменяется от ![]() до
до ![]() Величина
Величина
![]() называется девиацией частоты. Отсюда следует,
что
называется девиацией частоты. Отсюда следует,
что ![]() .
.
Если
![]() ,
(6)
,
(6)
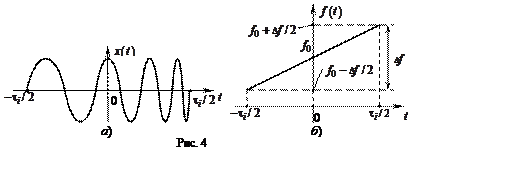 то
амплитудно-частотный спектр радиоимпульса близок к прямоугольному, а его ширина
П=
то
амплитудно-частотный спектр радиоимпульса близок к прямоугольному, а его ширина
П=![]() . Сигналы, для которых выполняется условие
(6), называются широкополосными.
. Сигналы, для которых выполняется условие
(6), называются широкополосными.
Следовательно, при выполнении условия (6) ЛЧМ радиоимпульс будет широкополосным. Комплексная амплитуда ЛЧМ радиоимпульса имеет вид:
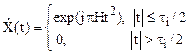 .
(7)
.
(7)
Преобразование
Фурье от ![]() определяет частотный спектр комплексной амплитуды
сигнала.
определяет частотный спектр комплексной амплитуды
сигнала.
Пример амплитудно-частотного спектра ЛЧМ-сигнала для В=30 приведен на рис.3.
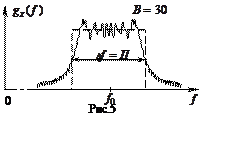 В ИС
находят применение импульсные и непрерывные фазоманипулированные
радиосигналы. Рассмотрим вначале радиоимпульсы с внутриимпульсной фазовой
манипуляцией.
В ИС
находят применение импульсные и непрерывные фазоманипулированные
радиосигналы. Рассмотрим вначале радиоимпульсы с внутриимпульсной фазовой
манипуляцией.
Структуру
радиоимпульса поясним следующим образом. Узкополосный немодулированный радиоимпульс
длительностью ![]() разделим на n
равных частей, каждая из которых будет представлять более короткий радиоимпульс
длительностью
разделим на n
равных частей, каждая из которых будет представлять более короткий радиоимпульс
длительностью
![]() .
(8)
.
(8)
Эти короткие импульсы принято называть парциальными.
 Фазовая
манипуляция сводится к изменению
начальных фаз парциальных радиоимпульсов по определенному закону. Обычно начальные
фазы парциальных импульсов принимают некоторый дискретный набор значений начальных
фаз в пределах
Фазовая
манипуляция сводится к изменению
начальных фаз парциальных радиоимпульсов по определенному закону. Обычно начальные
фазы парциальных импульсов принимают некоторый дискретный набор значений начальных
фаз в пределах ![]() . На практике получили
распространение ФМ сигналы с двумя значениями фаз преимущественно 0 и
. На практике получили
распространение ФМ сигналы с двумя значениями фаз преимущественно 0 и ![]() . Таким образом, ФМ радиоимпульсы можно
трактовать как последовательность сомкнутых немодулированных радиоимпульсов,
начальные фазы которых изменяются по определенному закону. Этот закон называют
кодообразующей последовательностью.
. Таким образом, ФМ радиоимпульсы можно
трактовать как последовательность сомкнутых немодулированных радиоимпульсов,
начальные фазы которых изменяются по определенному закону. Этот закон называют
кодообразующей последовательностью.
В случае, если
начальные фазы принимают лишь два значения, кодообразующая последовательность
может быть записана в виде последовательности нулей и единиц. Нулю
соответствует фаза 0, а единице - ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.