Исследование время-частотных характеристик сигналов: Методические указания к лабораторной работе по курсу "Обработка сигналов и изображений", страница 2

Сказанное поясняется рис.6. На нем изображен семиэлементный ФМ радиоимпульс. В четвертом, пятом и седьмом парциальных радиоимпульсах начальные фазы изменены на , как показано в первой строке таблицы. Во второй строке приведена кодообразующая последовательность. Применяются и другие обозначения кода, что поясняется третьей и четвертой строками таблицы.

Комплексная амплитуда ФМ сигнала с манипуляцией 0,  действительна. Для приведенного примера она изображена на рис.6. Запишем комплексную амплитуду первого парциального импульса в виде

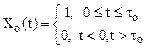.                                          (9)

Тогда комплексную амплитуду ФМ сигнала можно записать как

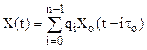,                                           (10)

где последовательность  в виде  (четвертая строка таблицы рис. 6 описывает код сигнала.

Если частотный спектр первого парциального импульса

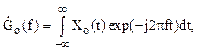                                    (11)

то спектр ФМ сигнала будет

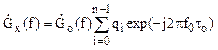.                                 (12)

На рис.7 в качестве примера изображен амплитудно-частотный спектр ФМ радиосигнала. Видно, что его ширина определяется длительностью парциального импульса

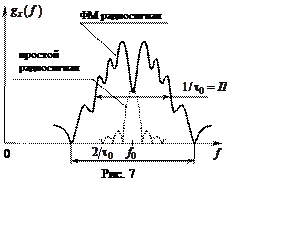
.                        (13)

База сигнала

.                      (14)

При достаточно большом числе парциальных импульсов сигнал будет широкополосным.

Если число парциальных импульсов ФМ сигнала n>>1, а кодообразующая последовательность достаточно “хаотична”, то сигнал называют шумоподобным.

Кодирование начальных фаз дискретов чаще всего осуществляется в соответствии с кодами Баркера и М-кодами. Коды Баркера найдены для . Сводка известных баркеровских кодовых последовательностей приведена в табл 1. Здесь парциальные радиоимпульсы с неизменной и измененной на  начальной фазой схематически показаны знаками плюс и минус.

Для непрерывных и имеющих большую длительность фазоманипулированных сигналов обычно используют периодические кодообразующие последовательности, составленные по определенному правилу. Широкое распространение получили так называемые М-коды или линейные рекуррентные последовательности максимальной длины.

Таблица 1.

Код Баркера	Кодирующая последовательность
3	0 0 1
4	0 0 1 0
5	0 0 0 1 0
7	0 0 0 1 1 0 1
11	0 0 0 1 1 1 0 1 1 0 1
13	0 0 0 0 0 1 1 0 0 1 0 1 0

3. ИССЛЕДОВАНИЕ ВРЕМЯ-ЧАСТОТНЫХ ХАРАКТЕРИСТИК СИГНАЛОВ СРЕДСТВАМИ MATLAB

3.1. Исследование время-частотных характеристик простых сигналов без внутриимпульсной модуляции

Файл-сценарий исследования время-частотных характеристик простых сигналов без внутриимпульсной модуляции имеет вид (PRIP.m)

t=0:0.01:0.3; %Задание длительности сигнала

N=20;         %Сдвиг по оси времени

f=20;         %Несущая частота

x=zeros(1,N);

y=sin(2*pi*f*t);  % формирование сигнала

y1=[x y x];

y11=fft(y1,512);   % ДПФ

G11=y11.*conj(y11)/512;

f=100*(0:255)/512;

subplot(2,1,1),plot(1:length(y1),y1), ylabel('y1(n)'); %Визуализация сигнала

                                                                                            на оси времени

subplot(2,1,2),plot(f,G11(1:256))   % Визуализация сигнала на оси частот

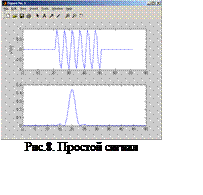
Результаты расчета время-частотных характеристик простых радиосигналов, при указанных в файле-сценарии параметрах, представлены на рис. 8.

Файл-сценарий исследования видеосигнала имеет следующий вид (PVC.m):

N=100;

x=zeros(1,N);              % Начало видеосигнала

y=[1 1 1 1 1 1 1 1 1 1];   % Длительность видеосигнала

y1=[x y x];                % Формирование видеосигнала

y11=fft(y1,512);           % Частотные свойства сигнала

G11=y11.*conj(y11)/128;

f=10*(0:255)/512;

subplot(2,1,1),plot(1:length(y1),y1),ylabel('y1(n)'); %Визуализация сигнала на

                                                                                            оси времени

subplot(2,1,2),plot(f,G11(1:256)) % Визуализация сигнала на оси частот

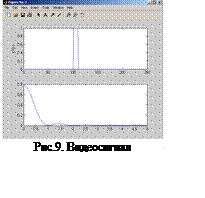
Результаты расчета время-частотных характеристик видеосигнала, при указанных в файле-сценарии параметрах, представлены на рис. 9.

3.2. Исследование время-частотных характеристик ЛЧМ сигналов

Файл-сценарий исследования время-частотных характеристик ЛЧМ сигналов имеет вид (LCHM.m)

t1=2;          % Длительность сигнала

ff=20;         % Девиация частоты

t=0:0.01:t1;   % временная дискретизация сигнала

N=20;

f=5;           % Несущая частота

x=zeros(1,N);

y=cos((2*pi*f*t+pi*(ff/t1)*t.^2)); % Формирование ЛЧМ сигнала