Расчет системы подчиненного регулирования электроприводом постоянного тока: Методические указания к выполнению курсового проекта по учебной дисциплине «Системы управления электроприводов»

Федеральное агентство по образованию

ГОУ ВПО «Сибирский государственный

 индустриальный университет»

Кафедра автоматизированного электропривода

и промышленной электроники

РАСЧЕТ СИСТЕМЫ

 ПОДЧИНЕННОГО РЕГУЛИРОВАНИЯ

ЭЛЕКТРОПРИВОДОМ ПОСТОЯННОГО ТОКА

Методические указания к выполнению курсового проекта

 по учебной дисциплине «Системы управления электроприводов»

 для студентов специальности 140604 «Электропривод и автоматика промышленных установок и технологических комплексов»

Новокузнецк

2006

          УДК 62-83-52(075)

          Расчет системы подчиненного регулирования электроприводом постоянного тока: Методические указания к выполнению курсового проекта по учебной дисциплине «Системы управления электроприводов» для студентов специальности 140604: Метод. указ. / Сост.: А.К. Мурышкин, С.А. Дружилов, Т.В. Богдановская – СибГИУ, Новокузнецк, 2006. -    с.

          Рассмотрены конкретные примеры расчета системы подчиненного регулирования и анализа качества регулирования, выполненные различными методами, в том числе, с использованием персонального компьютера.

          Предназначены для студентов специальности «Электропривод и автоматика промышленных установок и технологических комплексов» (140604) всех форм обучения.

          Рецензент – кафедра электротехники и электрооборудования Сибирского государственного индустриального университета (зав. кафедрой М.В. Кипервассер)

          Печатается по решению редакционно-издательского совета университета

ОБЩИЕ ПОЛОЖЕНИЯ МЕТОДИКИ РАСЧЕТА

          Особенностью данного направления в проектировании систем электропривода является раздельное подчиненное регулирование основных параметров электропривода, когда число последовательно-каскадно включенных регуляторов равно числу регулируемых координат. Задача заключается в оптимальном выборе параметров регуляторов, при котором регулируемый параметр реагирует на изменение задающего воздействия без запаздывания и без колебаний. Препятствием к достижению этого являются инерционности объекта и невозможность практической реализации бесконечных форсировок с сохранением достаточной помехоустойчивости.

          В большинстве практических случаев за оптимальную принимают такую настройку контура системы регулирования, при которой обеспечивается отработка задающего воздействия за минимальное время при перерегулировании выходной координаты около 5 %. Если в области рабочих частот модуль передаточной функции контура близок к единице, то всюду, кроме начального интервала времени, динамическая погрешность регулирования будет близка к нулю. Такую настройку контура называют настройкой на модульный оптимум (МО). Каждый контур системы регулирования может быть структурно расчленен на регулятор с передаточной функцией  и объект регулирования  [3, 4].

          Рассмотрим контур (рисунок 1).

          Если объект регулирования содержит одну большую инерционность и одну малую , то для настройки контура на МО достаточно ввести в него интегрально-пропорциональный (ИП) регулятор, имеющий передаточную функцию

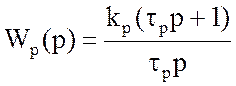                                                                                  (1)         

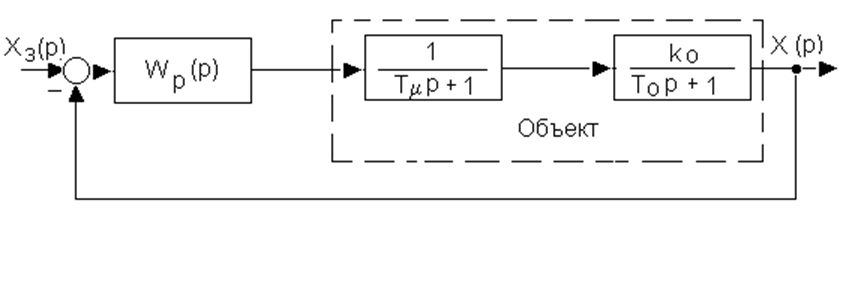Рисунок 1 – Схема оптимизированного контура

и выбрать его параметры следующим образом:

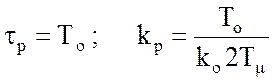                                        .                                (2)

          Передаточная функция замкнутого контура при указанных параметрах будет равна

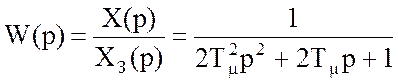                                .                         (3)

          Такая настройка обеспечивает стандартное демпфирование 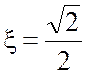, перерегулирование , время первого согласования , а время переходного процесса (время регулирования) . Однако, если в объекте имеется интегрирующее звено, то настройкой на МО достичь указанных показателей качества не удается. Здесь оптимальной считается такая настройка, при которой на частоте среза ЛАХ разомкнутой САУ симметрична относительно оси частот (рисунок 2). Эта настройка известна как симметричный оптимум (СО).

          Если в этом случае применить ИП-регулятор с передаточной функцией

,

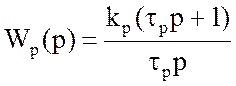то должны быть выполнены условия:

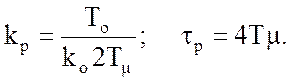
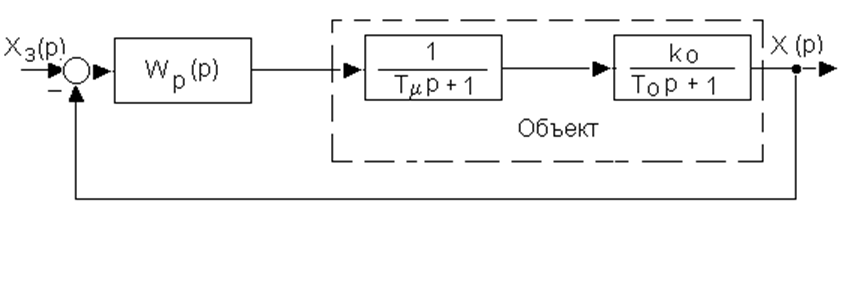Рисунок 2 – Контур с интегрирующим звеном

          Передаточная функция оптимизированного по условиям СО контура запишется в виде:

                       

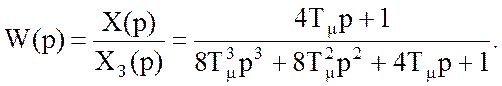
          Показатели качества процесса регулирования:

          Величину перерегулирования можно уменьшить до 8%, установив на входе контура регулирования фильтр с постоянной времени, равной  Тогда переходный процесс имеет следующие показатели:

          Вопрос о выборе типа регулятора и критерия настройки решается в каждом конкретном случае с учетом требований, предъявляемых к электроприводу рабочим механизмом.

РАЗОМКНУТАЯ СИСТЕМА

 «ВЕНТИЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ-ДВИГАТЕЛЬ (ВП-Д)»

Вентильный преобразователь без учета инерционности системы импульсно-фазового управления (СИФУ) с достаточной для инженерной практики точностью может быть представлен типовым звеном чистого запаздывания 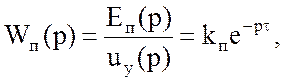[5]:

                                                                          (5)

где ЭДС преобразователя;

       управляющее напряжение;

       коэффициент передачи преобразователя;

        среднестатистическое запаздывание, определяемое неполной управляемостью вентилей, зависящее от частоты сети  и фазности преобразователя m.

          Запаздывание преобразователя невозможно компенсировать по его физической природе.