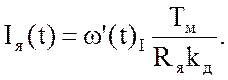 (39)
(39)
Установившийся ток при пуске получается после затухания свободных составляющих движения:
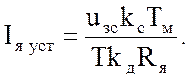 (40)
(40)
Следовательно,
при заданных параметрах электропривода ![]() величина
пускового тока зависит от соотношения
величина
пускового тока зависит от соотношения ![]() ,
которое остается постоянным при пуске, независимо от того, до какого значения
скорости производится разгон двигателя.
,
которое остается постоянным при пуске, независимо от того, до какого значения
скорости производится разгон двигателя.
Анализ
выражения (38) позволяет заключить, что при ![]() закон
изменения
закон
изменения ![]() линейный:
линейный:
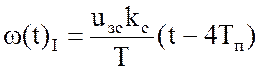 . (41)
. (41)
Чтобы
построить переходный процесс при ![]() , применяют следующий
прием: считают, что в этом случае система находится как бы
под воздействием двух сигналов: нарастающего
, применяют следующий
прием: считают, что в этом случае система находится как бы
под воздействием двух сигналов: нарастающего ![]() и убывающего
с той же интенсивностью
и убывающего
с той же интенсивностью ![]() (пунктирные линии на
рисунке 17) [2].
(пунктирные линии на
рисунке 17) [2].
Этот прием дает следующие результаты:
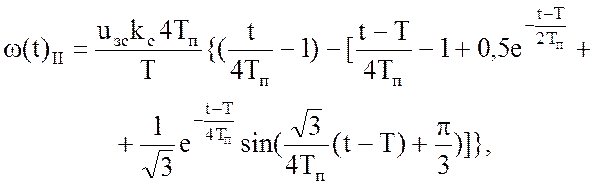 (42)
(42)
где t – текущее время, начиная с момента пуска двигателя.
Согласно (39), получим переходную характеристику для тока:
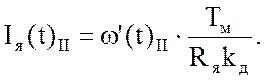
Динамика систем со специальными законами изменения выходного напряжения задатчика интенсивности выходит за рамки этих методических указаний. Методика расчета переходных процессов и в таком случае ничем не будет отличаться от изложенной.
Приложение нагрузки в однократно интегрирующей системе
Операторное уравнение, описывающее динамику рассматриваемой системы, имеет вид:
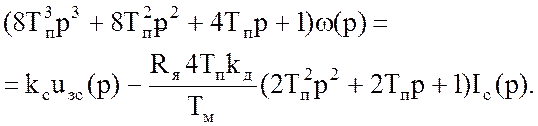 (43)
(43)
Изображение
(в приращениях) реакции системы на возмущающее воздействие (ток нагрузки ![]() запишем как
запишем как
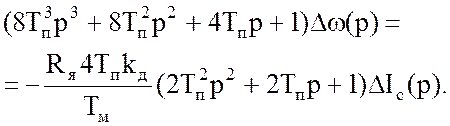 (44)
(44)
Временной закон изменения скорости найдем, используя [7]:
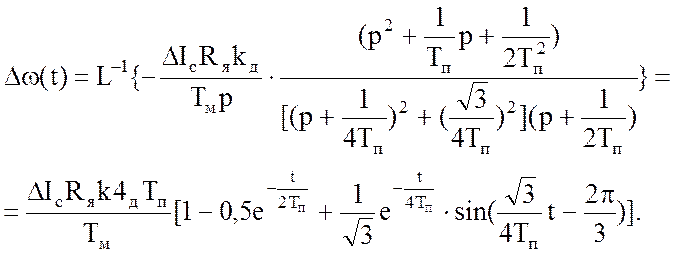 (45)
(45)
Учитывая, что
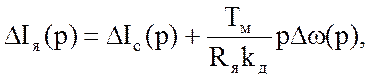
и
подставляя ![]() в это выражение из (45), найдем
изображение тока:
в это выражение из (45), найдем
изображение тока:
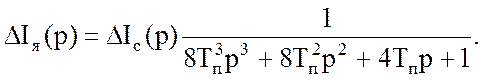
Изменение тока якоря при набросе нагрузки может быть найдено уже известным способом:
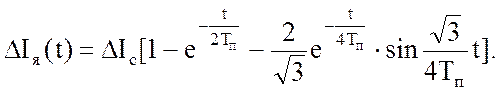 (47)
(47)
Из
выражения (45) получим статизм однократно интегрирующей системы при ![]() :
:
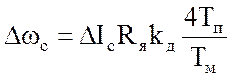 .
.
Переходные процессы в двукратно интегрирующей
системе электропривода ВП-Д
Установка на входе системы (рисунок 11) фильтра с
постоянной времени ![]() приводит к упрощению
передаточной функции оптимизированной по симметричному оптимуму системы:
приводит к упрощению
передаточной функции оптимизированной по симметричному оптимуму системы:
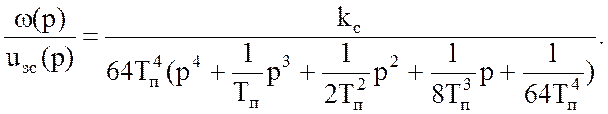 (48)
(48)
Корни характеристического полинома такой системы
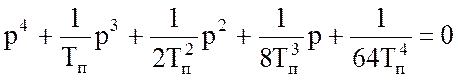
комплексные сопряженные:
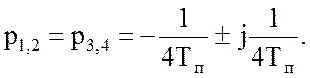
Разложив на множители знаменатель передаточной функции (48), получаем:
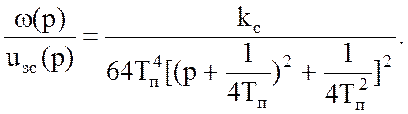 (49)
(49)
Реакцию
системы четвертого порядка на единичное скачкообразное воздействие ![]() определим так:
определим так:
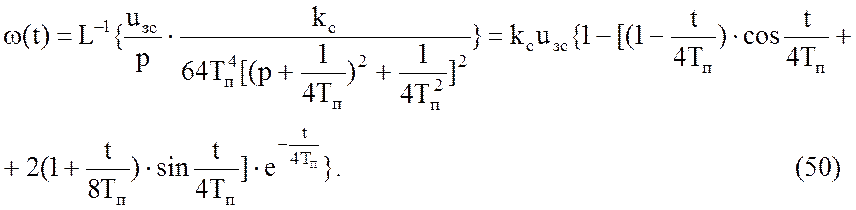 Время переходного процесса, судя
по (50), составляет около (12…14)
Время переходного процесса, судя
по (50), составляет около (12…14)![]() , перерегулирование равно
8%. Это говорит о высоком быстродействии оптимизированной системы и отсутствии
ограничения на величину тока (момента) двигателя при пуске. Для регламентации
ускорения электропривода на вход оптимизированной системы с фильтром включают
задатчик интенсивности, у которого выходное напряжение изменяется по линейному
закону.
, перерегулирование равно
8%. Это говорит о высоком быстродействии оптимизированной системы и отсутствии
ограничения на величину тока (момента) двигателя при пуске. Для регламентации
ускорения электропривода на вход оптимизированной системы с фильтром включают
задатчик интенсивности, у которого выходное напряжение изменяется по линейному
закону.
Изображение скорости при этом
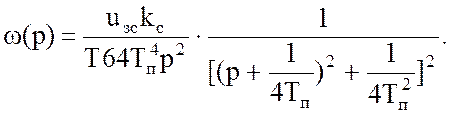
Переходный процесс найдем, используя таблицу обратных преобразований Лапласа [7]:
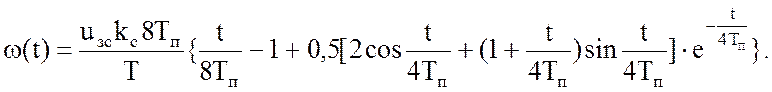 (51)
(51)
Выражение для тока якорной цепи имеет вид:
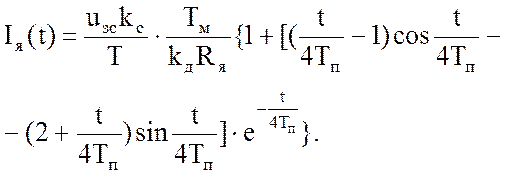 (52)
(52)
Это первый этап переходного процесса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.