tg y =m, т. е. получаем, что y=arctg m. Степень затухания рассматриваемой составляющей процесса будет определяться значением тангенса этого угла. Если корень характеристического уравнения pi=-a±jw этой системы будет лежать в плоскости комплексного переменного на линии АОВ, то степень затухания Y будет постоянной.
Между степенью затухания и степенью колебательности переходного процесса регулирования существует следующая зависимость:
где 2mp - логарифмический декремент затухания колебаний.
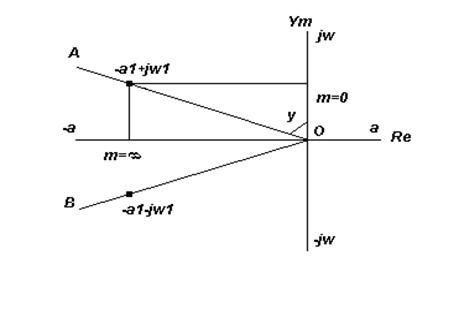
Рис 4.2.1 К пояснению понятия степени колебательности и степени затухания.
Выражение передаточной функции звеньев, для которых рi находится на линии АОВ, называется расширенной АФЧХ:
,
Если m=0, то РАФЧХ совпадает с линией АОВ и совмещается с мнимой осью, следовательно, АОВ – мнимая ось, а система находится на границе устойчивости.
Если m=∞, то РАФЧХ совмещается с действительной осью, что соответствует апериодическому переходному процессу.
Исходным условием при расчете оптимальных параметров настройки является соотношение:
т.е. произведение РАФХ объекта и регулятора равно единице.
Когда необходимо определить параметры настройки регулятора, обеспечивающие заданную степень затухания, производится замена p=(j-m)w. Смысл этой замены заключается в том, что корни характеристического уравнения имеют отрицательные части, а численное значение его обеспечивает заданный запас устойчивости, степень колебательности и затухания. Введение подобной замены есть ни что иное, как переход к расширенным АФХ.
Передаточная функция объекта, найденная при помощи самого точного метода:
Выбран ПИ- закон регулирования с передаточной функцией: Wp(p)= 
Примем m = 0,221, что соответствует значению степени затухания y=0,75.
a) Путем замены р=(j-m)w определяем РАФЧХ объекта, разлагая на мнимую и действительную части:
=
-
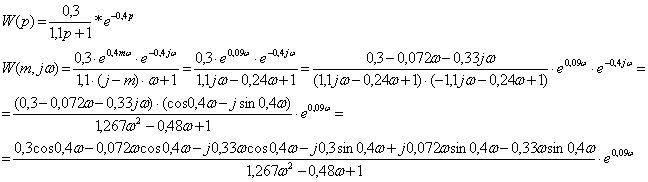
расширенная действительная частотная характеристика объекта.
=
- расширенная мнимая частотная
характеристика объекта.
b) Аналогичным образом переходят к расширенным АФЧХ регулятора, также разделяя действительную и мнимую части:
Wp(p)=
Wp(
)=
=
=
c) Исходя из условия 
имеем [
]*[
]=1
Преобразуем данную
функцию в систему уравнений:
|
(m,w) Re
(m,w) - Im(m,w) Im(m,w) – 1 = 0Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.