Параметрический синтез локальных систем автоматического управления, страница 6

       Используя данные таблицы 2.2.1, построим график функции ln|y₁(t_i)| и проведем асимптоту, которая отсекает на оси ординат lnC₁=1, а на оси абсцисс t^/₁=0,5 мин (рисунок 2.2.2).

t^/_i- отрезок времени, отсекаемый асимптотой на оси абсцисс.

а₁==      

 =>                                   

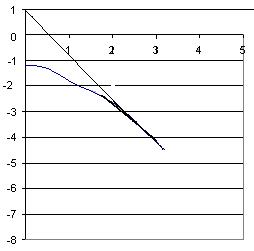
Рисунок 2.2.2 – Определение а₁ и С₁ методом последовательного

                                        логарифмирования

      Из графика видно, что функция ln|y₁(t_i)| и ее асимптота не совпадают на участке 0…1,25 мин. Следовательно, кривую разгона объекта нельзя аппроксимировать решением дифференциального уравнения первого порядка. Поэтому порядок уравнения повышаем до второго. Для решения поставленной задачи необходимо вычислить функцию невязок y₂(t) (таблица 2.2.1).

       Опять строим график функции ln|y₂(t)| и проводим к нему асимптоту (рисунок 2.2.3). Это позволяет вычислить а₂ и С₂:

а₂==      

 =>   

                                                                            

 

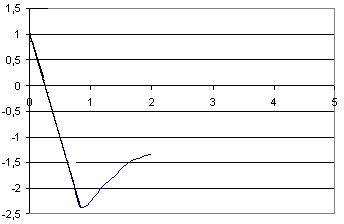
Рисунок 2.2.3 - Определение а₂ и С₂ методом последовательного

                                        логарифмирования

       Из рисунка 2.2.3 видно, что функция y₂(t) и ее асимптота хорошо совпадают на всем временном интервале. Поэтому окончательно принимаем порядок аппроксимирующего дифференциального уравнения n=2:

 

       Правильно ли определены С₁ и С₂ проверим по условию:

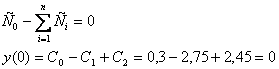
       Передаточная функция имеет следующий вид:

     

       Задав передаточную функцию объекта с помощью программного обеспечения Excel, построим расчетную характеристику.

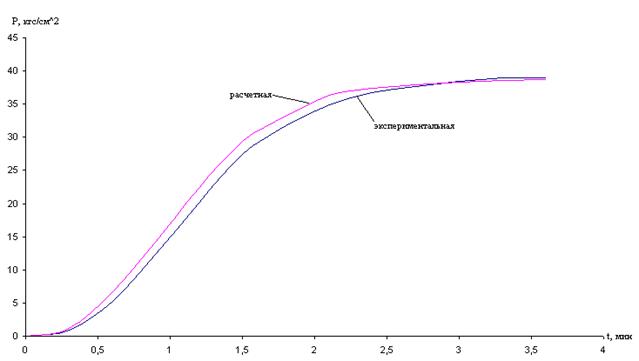
Рисунок 2.2.5 – Расчетная кривая, построенная с учетом запаздывания

- ошибка идентификации

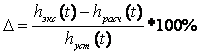
Таблица 2.2.2 – Ошибка идентификации

t	0	0,3	0,6	0,9	1,2	1,5	1,8	2,1	2,4	2,7	3	3,3	3,6
h(t)эксп	0	0,9	5,3	12,3	20,1	27,4	31,8	34,9	36,8	37,7	38,5	39	39
h(t)расч	0	1,2	6,7	14,2	22,3	29,4	33,2	36,3	37,3	37,9	38,4	38,6	38,8
D	0	-0,769	-3,59	-4,87	-5,64	-5,13	-3,59	-3,59	-1,28	-0,51	0,256	1,026	0,513