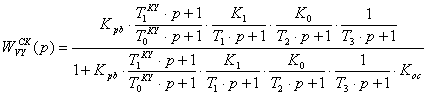
Учитывая соотношение ![]() и приводя к общему знаменателю,
получим:
и приводя к общему знаменателю,
получим:
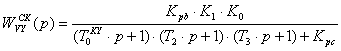 (5.8)
(5.8)
На основе (5.8) можно записать изображение выходного сигнала:
![]() (5.9)
(5.9)
Полагая
![]() , для структурной схемы (см. рисунок
5.2) можно записать передаточную функцию скорректированной системы по
возмущающему воздействию:
, для структурной схемы (см. рисунок
5.2) можно записать передаточную функцию скорректированной системы по
возмущающему воздействию:
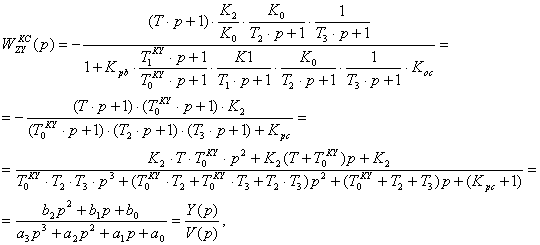
![]() (5.10)
(5.10)
где
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
На основе (5.10) можно записать изображение выходного сигнала:
![]() (5.11)
(5.11)
Используя принцип суперпозиции, с учетом (5.9) и (5.11) можно записать изображение выходного сигнала скорректированной системы
![]()
(5.12)
5.2 Анализ устойчивости скорректированной системы.
5.2.1 Устойчивость системы по критерию Гурвица.
Поскольку устойчивость системы не зависит от вида рассматриваемого входного сигнала, то положим Z=0.Тогда анализ устойчивости можно проводить на основе структурной схемы представленной на рисунке 5.3.
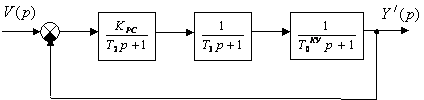 |
Рисунок 5.3 - Структурная схема скорректированной системы 2.
Передаточная функция в замкнутом состоянии:
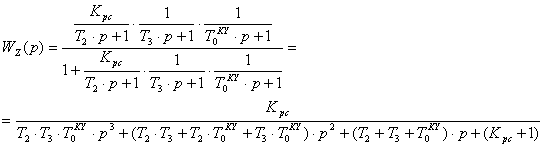 (5.13)
(5.13)
Прировняв к нулю знаменатель, можно записать характеристическое уравнение вида:
![]() (5.14)
(5.14)
где ![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
(5.15)
.
(5.15)
С учетом исходных данных (см. таблицу 1.1) и (5.15), (2.9) можно рассчитать коэффициенты характеристического уравнения исходной системы в замкнутом состоянии:
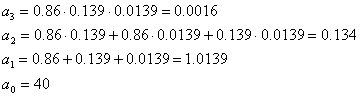
Для характеристического уравнения системы в замкнутом состоянии(4.1) можно записать главный определитель Гурвица 3-его порядка:
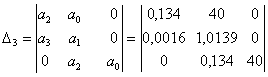 |
![]()
![]() ;
;
![]() ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.