Расчет системы автоматической стабилизации заданного значения выходной координаты (контрольная работа), страница 3

                (2.8)

На основе (2.8) можно записать систему уравнений:  

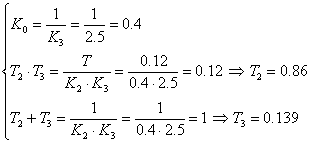                        (2.9)

                      

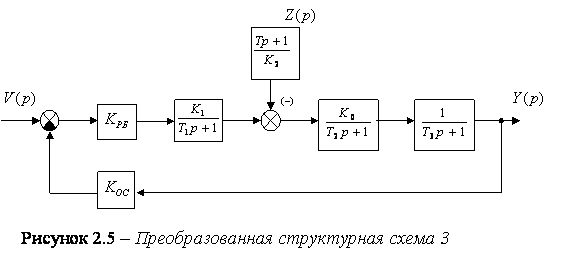
Передаточная функция по управляющему воздействию:

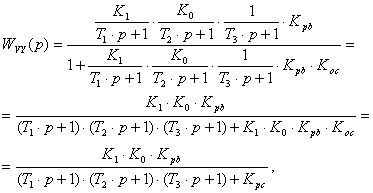                 (2.10)

  где  - передаточный коэффициент  разомкнутой системы.

Изображение выходного сигнала:            (2.11)

Для определения передаточной функции системы по возмущающему воздействию можно положить .

Передаточная функция по возмущающему воздействию:

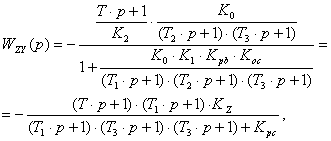                      (2.12)

где  передаточный коэффициент по возмущающему воздействию.

Изображение выходного сигнала:            (2.13)

Используя принцип суперпозиции, на основе (2.11) и (2.13) окончательно можно записать:

                                                     (2.14)

3. Статический расчет.

     Пусть . Значит рассмотрим исходную разомкнутую систему без обратной связи. Тогда на основе (2.14), с учетом теорем операционного исчисления о предельных значениях при  можно записать уравнение статики вида:

                            (3.1)

где  - полезная составляющая выходного сигнала в разомкнутой системе;

    =  - величина, на которую уменьшается выходной сигнал в разомкнутой системе из-за влияния возмущающего воздействия.

В  соответствии с таблицей (1.1) и формулой (3.1) можно рассчитать погрешность стабилизации выходного сигнала в разомкнутой системе:

  где  - максимальное значение возмущающего воздействия.

  В соответствии с (3.1) можно записать:

Пусть  

      Рисунок 3.1 – Статическая характеристика разомкнутой системы. 

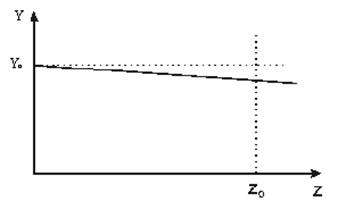Требуемая точность стабилизации выходной координаты в статическом режиме составляет . Поскольку , то разомкнутая система должна быть заменена замкнутой системой автоматической  стабилизации.

Подставляя  в (2.14), с учетом  и  можно записать:

,    (3.2)

где ,  =.

Поскольку задание на проектирование предполагает выполнение в замкнутой системе условия вида: