Расчет системы автоматической стабилизации заданного значения выходной координаты (контрольная работа), страница 4

,                           (3.3)

то используя знак равенства в (3.3), окончательно можно записать расчетную формулу требуемого значения передаточного коэффициента разомкнутой системы:

                    (3.4)

С учетом формулы  = = ,  на основе     (3.4)  можно рассчитать требуемое значение передаточного коэффициента решающего блока:

         

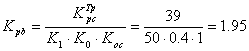
4 Анализ устойчивости исходной системы.

4.1 Устойчивость системы по критерию Гурвица.

      Устойчивость системы зависит от ее структуры и значения параметров элементов. Если система устойчива, то по любому воздействию переходные процессы затухающие, т.е. устойчивость не зависит от входных сигналов. Положим, что Z=0. Тогда структурная схема системы выглядит следующим образом:

Передаточная функция в замкнутом состоянии:

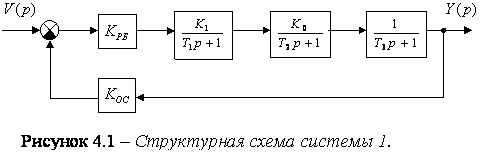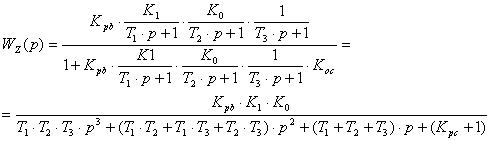
Прировняв к нулю знаменатель, можно записать характеристическое уравнение вида:

                                   (4.1)                  

где ,

          ,

          ,

          .                                                                                         (4.2)

С учетом исходных данных (см. таблицу 1.1) и (4.2), (2.9) можно рассчитать коэффициенты характеристического уравнения  исходной системы в замкнутом состоянии:

      

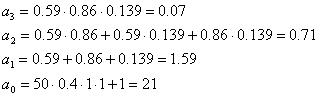
  Для характеристического уравнения системы в замкнутом состоянии(4.1) можно записать главный определитель Гурвица 3-его порядка:

          

;                                                                    

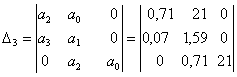
                        (4.3)

Так как по (4.3) определитель Гурвица 2-го порядка меньше нуля, то система в исходном состоянии неустойчива.

На основе (4.3) с учетом (4.2) можно записать граничное значение передаточного коэффициента системы в разомкнутом состоянии:

,                     (4.4)                                    где - граничное значение передаточного коэффициента системы в разомкнутом состоянии;

На основе(4.4) можно записать:

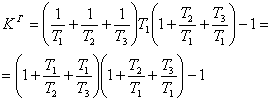                        (4.5)

Подставив значения  постоянных времени (см. таблицу 1.1 и (2.9)) в (4.5), можно получить искомую величину:

Так как  <  - система не устойчива.

4.2 Устойчивость системы по критерию Найквиста.

       Условием применения критерия является необходимость приведения исходной структурной схемы к одноконтурной структурной схеме с единственной связью вида с учетом соотношения между постоянными времени T2>T1>T3: