Расчет системы автоматической стабилизации заданного значения выходной координаты (контрольная работа), страница 2

В таблице 1.1 дополнительно введены следующие обозначения:

        - величина возмущающего воздействия;

        - требуемая точность стабилизации выходной координаты системы в       

                установившемся режиме.

2 Математическое описание системы.

2.1 Построение структурной схемы системы.

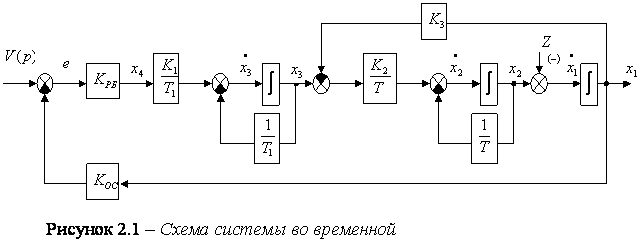
На основе уравнений (1.1) можно построить схему системы во временной форме (см. рисунок 2.1). На основе рисунка 2.1 можно построить структурную схему системы (см. рисунок 2.2)

 

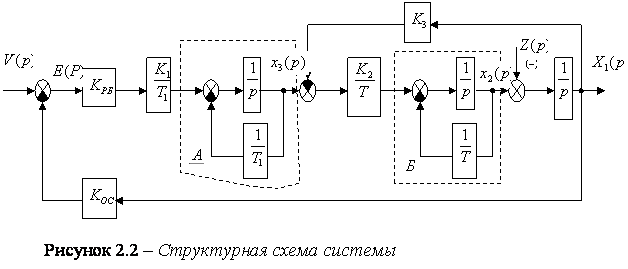
2.2 Определение передаточной функции системы по

управляющему и возмущающему воздействиям.

При исследовании линейных систем справедлив принцип суперпозиции: реакция системы на несколько одновременно действующих сигналов равна сумме реакций на каждый сигнал в отдельности.

         Используя формулы структурных преобразований для контура А можно записать:

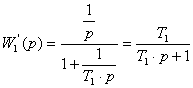                                                  (2.1)

Окончательно для  первого звена можно записать:

                                    (2.2)

 Передаточная функция (2.2) соответствует пропорциональному инерционному звену первого порядка.

Для контура Б можно записать:                                                                                   

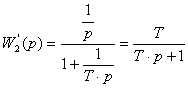                                                   (2.3)

Окончательно для  второго звена можно записать:

                                  (2.4)

Передаточная функция (2.4) соответствует пропорциональному инерционному звену первого порядка.

После преобразований передаточных функций можно представить структурную схему системы (см. Рисунок 2.3).

                      

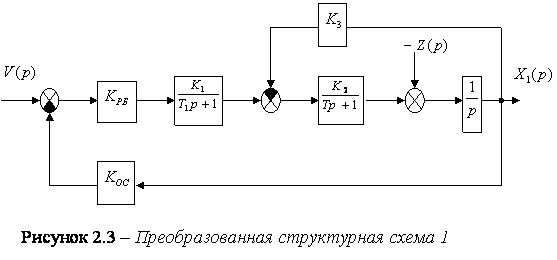
       Сумматор, на который подается возмущающее воздействие , целесообразно перенести против хода сигнала, при этом добавляется передаточная функция равная передаточной функции звена, через которое осуществляется перенос сигнала.

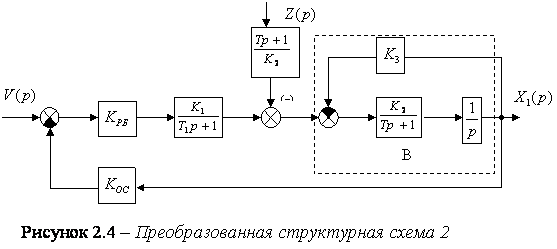
       Для определения передаточной функции системы по управляющему воздействию , в соответствии с принципом суперпозиции, полагают  .

Для контура В можно записать:

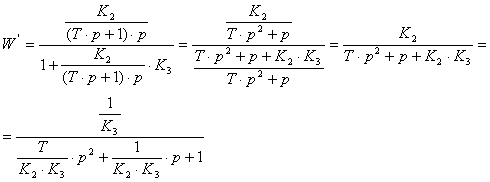                              (2.5)

       Формула (2.5)  передаточной функции пропорционального инерционного звена второго порядка.

       Приравняв знаменатель (2.5) к нулю, получили:

                              =0   или   ,               (2.6)

где ,   ,    .

Дискриминант:

       (2.7)

При условии (2.7) звено второго порядка может быть представлено последовательным соединением двух звеньев первого порядка, т.е.: