Синергетический подход к диагностике потерь эффективности, страница 8

При допущении о стационарности и эргодичности управляющего воздействия имеем, что ошибка идентификации на интервале NT_S является константой и равна:

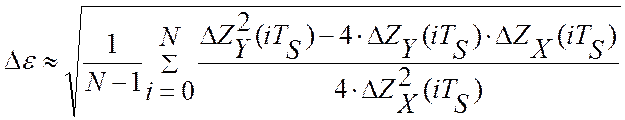                         (8.12)

Из выражения видно, что при стремлении  Nв бесконечность ошибка идентификации стремиться в ноль (см. рис. 3.10). Однако, в реальных условиях, имеются жёсткие ограничения на длину массивов, применяемых для идентификации свойств объекта управления. Из рисунка 3.10 видно, что при увеличении скорости дрейфа, α_дрi ,  длина массивов, участвующих в процессе идентификации должна быть уменьшена. При этом изменяется эффективность функционирования робастной системы и возникает потребность в адаптации настроечных коэффициентов виртуального прибора.  То есть существуют оптимальные значения, как темпа обработки информации, T_S⁰ , так и оптимальный объём выборки измерительной информации, N⁰ .

 

С учётом изложенного потери информации на одном интервале идентификации T_И=NT_S, можно вычислить по показаниям виртуального прибора (см. рисунок 3.11) следующим образом: 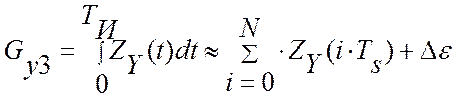                       , а общие потери на M интервалах идентификации, при этом,  будут равны:

                             ,

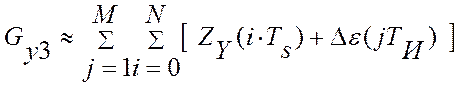где M  – это  число интервалов идентификации, T_S  - темп сбора текущих значений с датчиков измерительной информации,  T_И  – время идентификации;  N – длина массива показаний программно-аппаратного прибора,  - текущее значение критерия управления, измеренное виртуальным прибором.

 

 

X(t)

t

Kдр

                                                                                

							t

 

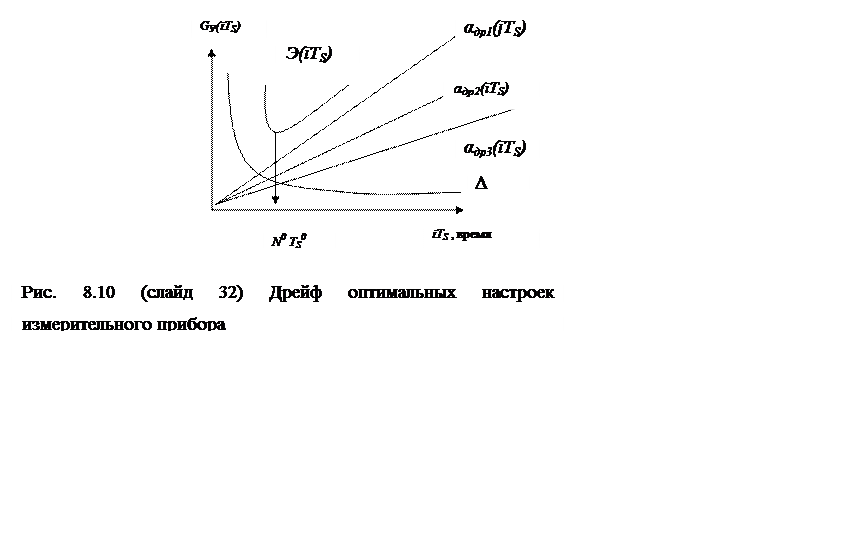
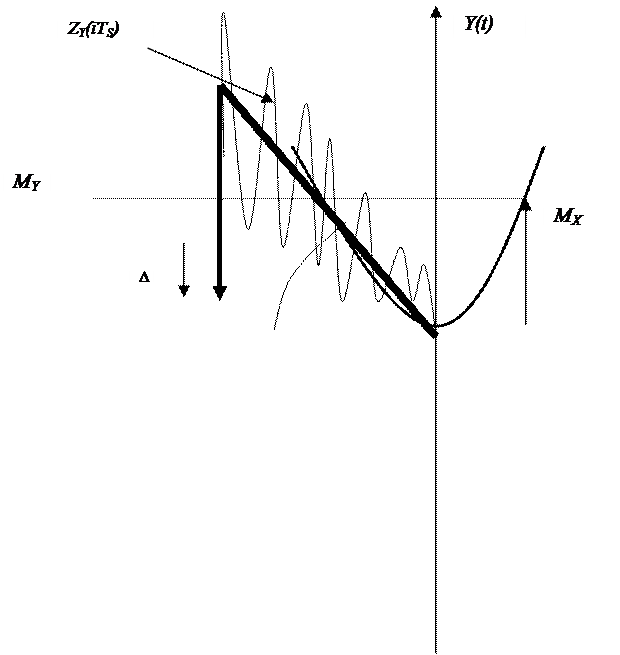
Рис. 8.11 (С.33) Формирование ошибки текущей идентификации

Как видно из рисунка 3.12  к потерям остаточного дрейфа робастных систем необходимо добавлять величину ошибки идентификации и тогда общие потери от остаточного дрейфа оценивать простой сумой показаний виртуального прибора.

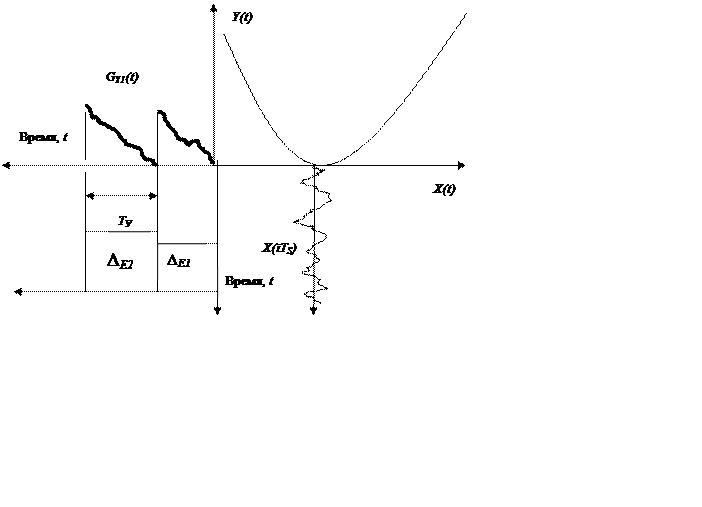
               Рис. 8.12. (С.34)  Образование ошибок идентификации

  Таким образом (см. рисунки 3.10 -:- 3.12), потери от неточности идентификации могут быть вычислены по соотношению:

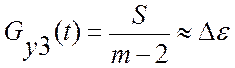                                           ,                           (8.13)        

где S– уровень помехи измерения управляющего воздействия, m – количество некоррелированных измерений управляющего воздействия. Это соотношение вытекает непосредственно из условия построения прямой по трем точкам, одна из которых является рабочей, а две другие являются ограничением на величину погрешности идентификации. На рисунке 3.10 пакет прямых линий характеризует процесс формирования потерь при случайной скорости дрейфа характеристик объекта управления, α_дрi. Из рисунка видно, что существуют оптимальный период опроса датчиков в процессе идентификации, T_S⁰ и  минимальный объем выборки измерительной информации для задач идентификации :   , где:  m – число некоррелированных интервалов измерения (количество интервалов некоррелированных измерений), которое определяется по постоянной времени автокорреляционной функции управляющего воздействия, T_XX . При этом число измерений, укладывающихся на одном интервале времени равному постоянной времени автокорреляционной функции управляющего воздействия, T_XX , должно быть не менее 10.

     Таким образом, величина погрешности идентификации, , зависит от конкретных условий цифровой обработки измерительной информации в информационно-измерительной подсистеме АСУТП и зависит, в первую очередь, от метода линеаризации критерия управления, метода моделирования случайных процессов и самого метода идентификации.