В этом и заключается
синергетический подход к оценке качества робастных систем управления, когда
все ресурсы системы управления (вычислительные возможности, интеллектуальные
возможности, технические возможности и др.) направлены на достижение одной цели
– обеспечения минимума потерь конкретного ресурса (или энергии), фиксируемого
критерием управления, Y(t), обеспечивая устойчивость всех переходных процессов. При
этом потери при адаптивном управлении необходимо рассматривать при условии
обеспечения оптимальных условий функционирования робастной системы, в основе
которой лежит критерий управления – эффективность функционирования объекта
управления, который гарантированно имеет минимум и может быть использован в
качестве критерия оптимальности функционирования робастной технической системы,
![]() (см. рис. 8.4).
(см. рис. 8.4).
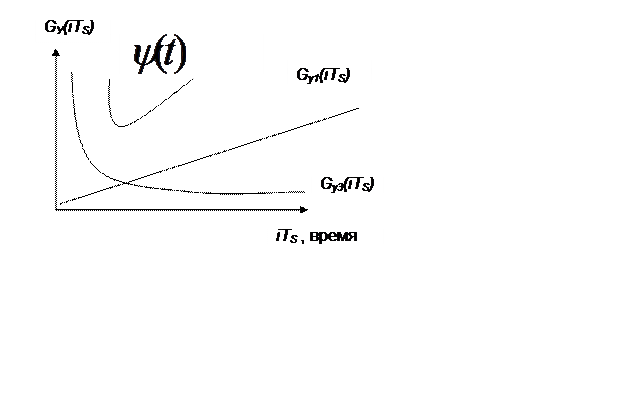 |
Рис.8.3. (С. 25) Геометрическая интерпретация эффективности технической системы
На рисунке 8.3 Gу1(iTS) – текущие значения потерь от остаточного дрейфа характеристик объекта управления, Gу3(iTS) – текущее значение неточности идентификации характеристик объекта и GУ(iTS) – текущее значение суммарных потерь. Общие потери качества робастной технической системы, как было показано выше, естественно оценивать суммой:
![]() ,
,
а эффективность алгоритмов управления,
![]() , при этом полностью определяется
показаниями виртуального прибора и его настроечными коэффициентами. а,
следовательно, эффективность функционирования алгоритмов может быть
оценена величиной отношения:
, при этом полностью определяется
показаниями виртуального прибора и его настроечными коэффициентами. а,
следовательно, эффективность функционирования алгоритмов может быть
оценена величиной отношения:
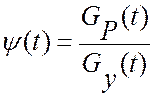 . (8.3)
. (8.3)
При этом эффективность робастной
технической системы с адаптивным управлением является функцией реального
времени и зависит только от настроек системы робастной стабилизации и от
настроек алгоритмов робастной системы управления. Критерий эффективности
функционирования робастной системы управления, ![]() ,
позволяет количественно оценить во сколько раз потери эталонной (аналоговой)
системы регулирования, GP(t), больше
потерь, образованных при работе робастной технической системы с адаптивным
управлением. Если
,
позволяет количественно оценить во сколько раз потери эталонной (аналоговой)
системы регулирования, GP(t), больше
потерь, образованных при работе робастной технической системы с адаптивным
управлением. Если ![]() ,
то потери системы оптимального управления и потери эталонной системы
сопоставимы, а, следовательно, применение системы оптимального управления не
эффективно. Если
,
то потери системы оптимального управления и потери эталонной системы
сопоставимы, а, следовательно, применение системы оптимального управления не
эффективно. Если ![]() , то система
оптимального управления эффективна. Если
, то система
оптимального управления эффективна. Если ![]() , то
более эффективно применение робастной стабилизации. Кроме того, по величине
критерия
, то
более эффективно применение робастной стабилизации. Кроме того, по величине
критерия ![]() можно сравнивать эффективность множества
алгоритмов и выбирать алгоритм, наиболее эффективно работающий в тех условиях,
на которые настроен виртуальный прибор, то есть с учётом динамических свойств
измерительной информации и объекта управления.
можно сравнивать эффективность множества
алгоритмов и выбирать алгоритм, наиболее эффективно работающий в тех условиях,
на которые настроен виртуальный прибор, то есть с учётом динамических свойств
измерительной информации и объекта управления.
Потери эффективности эталонного аналогового регулирования можно определить при допущения о том, что критерий управления, Y(t), дрейфует с постоянной скоростью K0, а об объекте управления мы знаем, что критерий управления имеет параболическую модель вида:
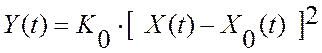 , (8.4)
, (8.4)
где X(t) – текущее значение управляющего воздействия; X0(t) – задание регулятору управляющего воздействия. Тогда (см. рисунок 8.4), качество эталонного регулирования, можно количественно оценить интегральным критерием качества:
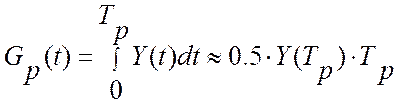 , (8.5)
, (8.5)
где Tр– время регулирования, Y(t) – показания эталонной измерительной системы.
Если обозначить количественную оценку нестационарного случайного процесса дрейфа объекта управления на интервале идентификации как Kдр, то текущее значение критерия управления можно записать в виде:
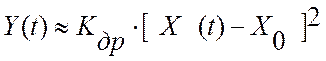 .
.
Пусть 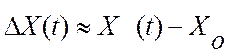 ,
тогда текущее значение скорости дрейфа критерия управления можно оценить
производной по времени:
,
тогда текущее значение скорости дрейфа критерия управления можно оценить
производной по времени:
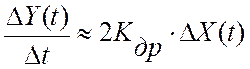 .
.
Выбирая время измерения равное 1
секунде ( ![]() ) получаем, что
) получаем, что ![]() , откуда текущее значение скорости
дрейфа критерия управления равно:
, откуда текущее значение скорости
дрейфа критерия управления равно:
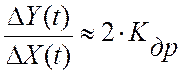 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.