Пусть критерий управления, Y(t), дрейфует со скоростью αдр(t), а об объекте управления мы знаем, что критерий управления имеет параболическую модель вида (3.6):
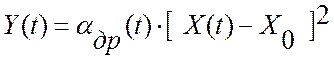 ,
,
где X(t) – текущие значения управляющего воздействия; X0 – задание адаптивному регулятору управляющего воздействия на интервале времени идентификации эталонной модели критерия управления, TИ = N·TС; αдр(t) – нестационарный случайный процесс характеризующий дрейф критерия управления.
Из рисунка 3.6 видно, что качество робастной стабилизации можно количественно оценить по интегральному критерию качества:
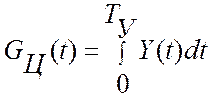 ,
,
где TУ – период управления; Y(t) – показания эталонной измерительной системы.
Пусть 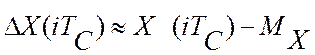 ,
тогда текущее значение скорости дрейфа критерия управления можно оценить
производной по времени:
,
тогда текущее значение скорости дрейфа критерия управления можно оценить
производной по времени: 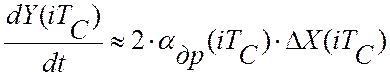 . Выбирая время
измерения равное 1 секунде (
. Выбирая время
измерения равное 1 секунде ( ![]() ) получаем, что
) получаем, что 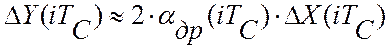 , откуда текущее значение скорости дрейфа
критерия управления равно:
, откуда текущее значение скорости дрейфа
критерия управления равно:
 . А
текущее значение дисперсии показаний цифрового эталонного прибора будет равно:
. А
текущее значение дисперсии показаний цифрового эталонного прибора будет равно: 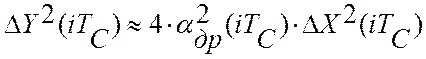 .
.
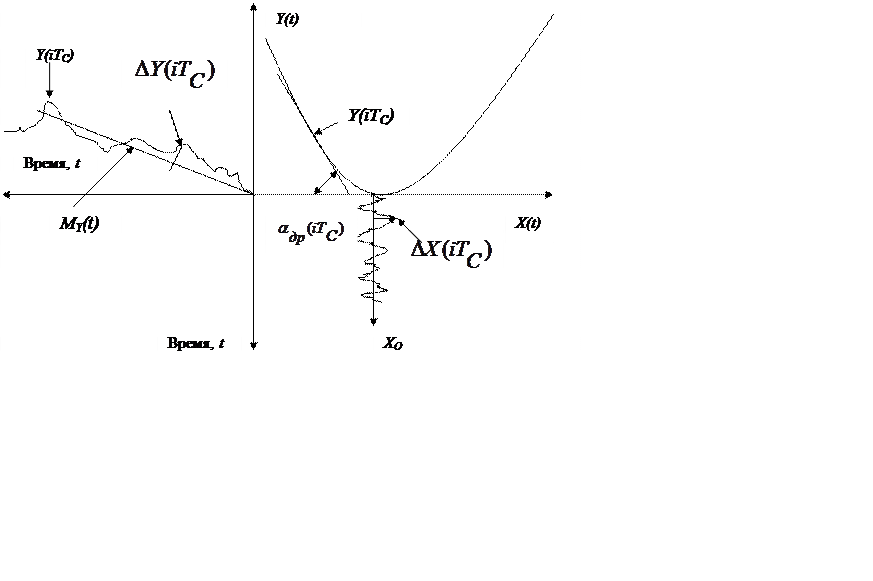
Рис. 8.6 (С. 28) Потери эффективности при робастной стабилизации
Текущее значение скорости дрейфа
критерия управления, 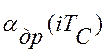 , можно оценить по текущему
значению взаимокорреляционной функции показаний эталонного цифрового прибора и
текущему значению дисперсии управляющего воздействия:
, можно оценить по текущему
значению взаимокорреляционной функции показаний эталонного цифрового прибора и
текущему значению дисперсии управляющего воздействия:
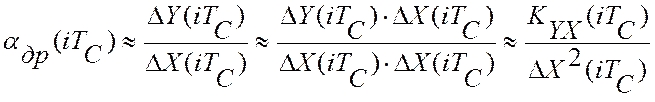
Эти оценки справедливы при усреднении по множеству реализаций. Учитывая, что управляющий параметр X(t) и критерий управления, измеренный с помощью виртуального прибора, Y(t) относятся к классу случайных стационарных эргодических процессов, усреднение можно провести по длине одной реализации и получить среднее значение скорости дрейфа на интервале идентификации, длинной N - измерений:
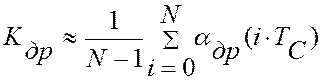
При этом, если дисперсию
последовательности показаний виртуального прибора
записать через дисперсию истинного значения измеряемой величины и
аддитивной помехи 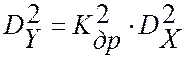 , то потери качества робастной
стабилизации можно определить через показания эталонного цифрового прибора Y(i·TC), ( см. рисунок 3.6) как:
, то потери качества робастной
стабилизации можно определить через показания эталонного цифрового прибора Y(i·TC), ( см. рисунок 3.6) как:
 ,
,
где TC – настроечный коэффициент модуля
ввода аналоговой информации; N –длина реализации показаний цифрового прибора; Y(iTC) – текущее значение показаний цифрового прибора,  - адаптивный настроечный коэффициент
системы робастной стабилизации (оценка скорости дрейфа).
- адаптивный настроечный коэффициент
системы робастной стабилизации (оценка скорости дрейфа).
Если инструментальную
составляющую потерь информации, на i-том шаге измерения, которая пропорциональна площади фигуры, заключённой
между истинным значением измеряемой величины на участке времени Tc и показанием виртуального прибора в
момент времени iTs,
обозначить как ![]() (см. рис.8.5), то дисперсию
инструментальной составляющей потерь можно вычислить как:
(см. рис.8.5), то дисперсию
инструментальной составляющей потерь можно вычислить как:
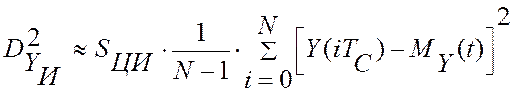 ,
,
где 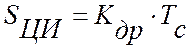 адаптивная
настройка цифрового прибора, зависящая от настроек модуля ввода аналоговой
информации,
адаптивная
настройка цифрового прибора, зависящая от настроек модуля ввода аналоговой
информации, 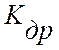 – статистическая оценка скорости дрейфа
критерия управления;
– статистическая оценка скорости дрейфа
критерия управления; ![]() – время измерения i-го значения измеряемой величины;
– время измерения i-го значения измеряемой величины; ![]() – i-тое показание цифрового прибора, регистрирующего текущие
значения критерия управления Y(t); MY(t)- оценка
математического ожидания критерия управления на интервале времени NTC . Исследования, проведённые в
работе [9] подтвердили, что этот тип потерь обусловлен квантованием по уровню и
у современных контроллеров < 10-4. Это позволяет формировать
массивы длиной 100 элементов с общей погрешностью представления информации <
0.1%, что вполне достаточно для промышленных алгоритмов идентификации.
– i-тое показание цифрового прибора, регистрирующего текущие
значения критерия управления Y(t); MY(t)- оценка
математического ожидания критерия управления на интервале времени NTC . Исследования, проведённые в
работе [9] подтвердили, что этот тип потерь обусловлен квантованием по уровню и
у современных контроллеров < 10-4. Это позволяет формировать
массивы длиной 100 элементов с общей погрешностью представления информации <
0.1%, что вполне достаточно для промышленных алгоритмов идентификации.
Методическая
составляющая потерь
информации на i-м шаге измерения ![]() пропорциональна площади фигуры,
заключённой между истинным значением измеряемой величины на участке времени (TS – Tc) и показанием цифрового прибора в момент времени iTs (см. рис. 3.5). Учитывая, что при
робастной стабилизации TS = TC , оценка дисперсии этой величины
потерь может быть вычислена по соотношению:
пропорциональна площади фигуры,
заключённой между истинным значением измеряемой величины на участке времени (TS – Tc) и показанием цифрового прибора в момент времени iTs (см. рис. 3.5). Учитывая, что при
робастной стабилизации TS = TC , оценка дисперсии этой величины
потерь может быть вычислена по соотношению:
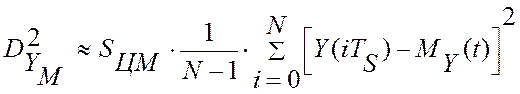 ,
,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.