Синергетический подход к диагностике потерь эффективности, страница 4

А текущее значение дисперсии показаний аналогового прибора будет равно:

                                       

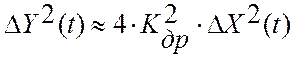
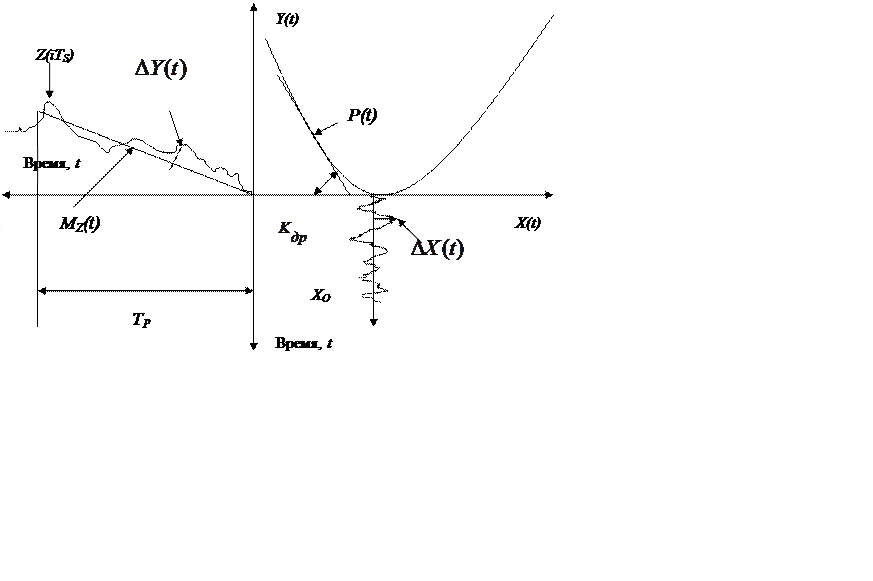
Рис8.4  (С.26) Процесс формирования потерь при аналоговом регулировании

        При цифровом эталонном регулировании текущее значение скорости дрейфа критерия управления можно оценить  по текущему значению взаимокорреляционной функции показаний эталонного цифрового прибора  и текущему значению отклонений управляющего воздействия от задания:

                     

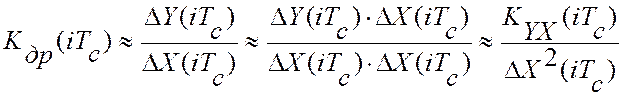
Эта оценка справедлива при усреднении по множеству реализаций. Учитывая, что управляющий параметр X(t)  и критерий управления, Y(t) относятся  к классу случайных стационарных эргодических процессов усреднение можно провести по длине одной реализации и получить среднее значение скорости дрейфа на интервале идентификации ( N  - длина массива):

                                                 

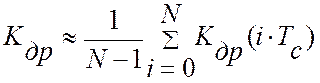
При этом, если дисперсию последовательности показаний эталонного прибора записать через дисперсию истинного значения измеряемой величины 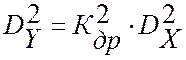, то потери качества эталонного цифрового регулирования можно определить через показания эталонного цифрового прибора Y(i·T_S), ( см. рис.3.4) как:

   ,                 

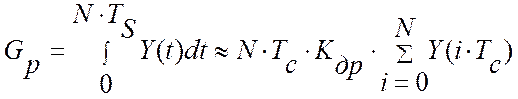где T_С     – настроечный коэффициент модуля ввода аналоговой информации;   N –длина реализации показаний эталонного прибора;  Y(iT_С) – текущее значение показаний эталонного цифрового прибора. 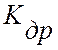-  адаптивный настроечный коэффициент эталонного цифрового регулирования (оценка скорости дрейфа на интервале идентификации).

Если инструментальную составляющую потерь информации, на i-том шаге измерения, которая пропорциональна площади фигуры, заключённой между истинным значением измеряемой величины на участке времени T_С , обозначить как  , то оценка дисперсии инструментальной составляющей потерь можно вычислить как:

                               ,

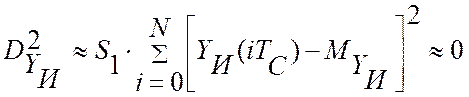где 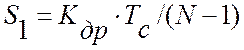 адаптивная настройка эталонного цифрового прибора, зависящая от настроек модуля ввода аналоговой информации,  – статистическая оценка скорости дрейфа критерия управления;   – время измерения i-го значения измеряемой величины;  – i-тое показание эталонного цифрового прибора, регистрирующего текущие значения критерия управления Y(t);   M_Yи - оценка математического ожидания на интервале времени t=NT_С .

        Исследования,  проведённые в работе [9] подтвердили, что этот тип потерь обусловлен квантованием по уровню и у современных цифровых приборов < 10^-10  и ими можно пренебречь, при построении оптимальных систем управления.

Методическая составляющая потерь информации на i-м шаге измерения эталонного прибора,  пропорциональна площади фигуры, заключённой между истинным значением измеряемой величины на участке времени (T_S – Tc) и показанием виртуального прибора в момент времени iT_s. Так как у цифровых приборов T_S=T_C , оценка дисперсии этой величины потерь может быть вычислена по соотношению:

,

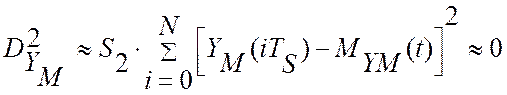где 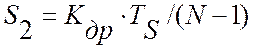 – адаптивная настройка эталонного цифрового прибора, зависящая от настроек модуля вывода аналоговой информации. Как правило, темп обработки информации, T_{S ,} в эталонном приборе, можно сделать равным времени измерения текущего значения измеряемой величины, T_C  (см. рис. 3.5). При этом, потери информации будут зависеть только от инструментальной составляющей погрешности цифровой обработки информации, S_И(iT_C). Дисперсия показаний эталонного цифрового  прибора будет  полностью определяться временем измерения, T_C ,  и длиной реализации (массива), N: 

                               

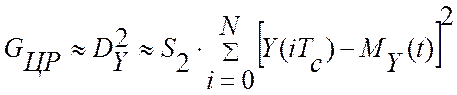
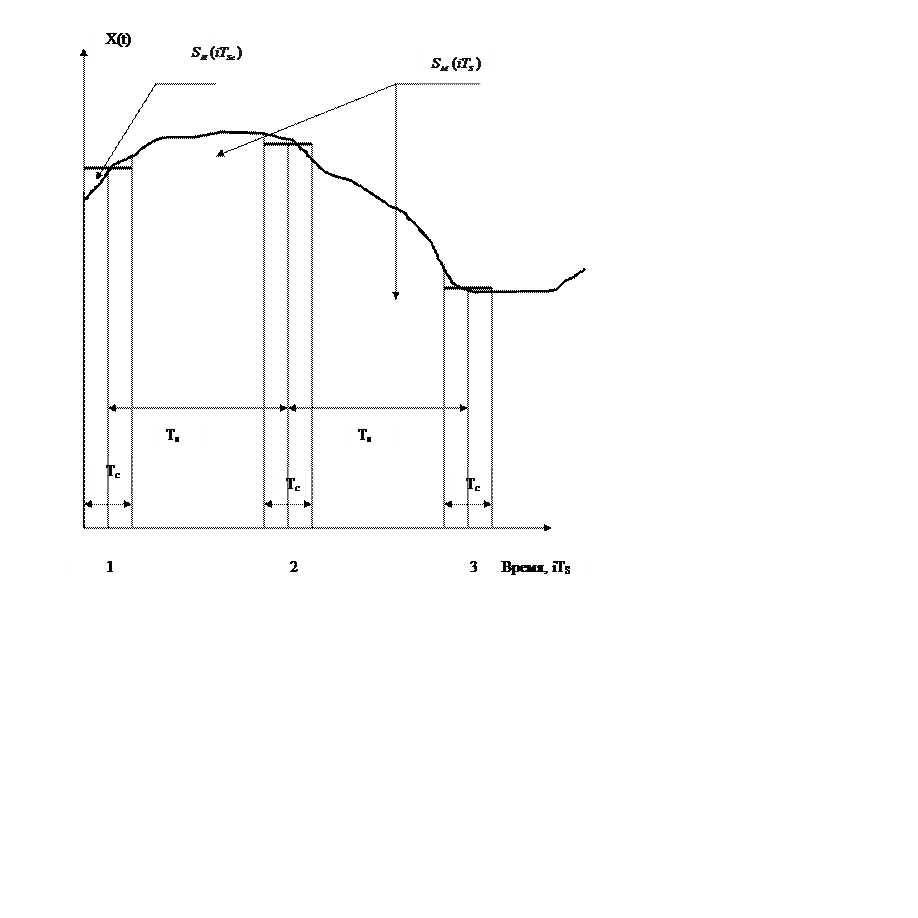Рис. 8.5. (С. 26) Потери информации в цифровых последовательностях

8.2 Диагностика эффективности при робастной стабилизации

         Пусть  – это текущее значение последовательности показаний эталонного цифрового прибора в i-й момент времени. При усреднении по ансамблю реализаций случайная составляющая методической динамической погрешности этих показаний будет равна текущему значению дисперсии показаний , при заданной длине реализации, N.

Пусть в результате параметрической оптимизации интеллектуальной измерительной системы по измерению критерия управления был найден оптимальный объём измерительной информации, N и период нанесения управляющего воздействия, T_У.