где αдр(iTS) – текущее значение скорости дрейфа критерия
управления. Из (3.8) следует, что текущее значение квадрата отклонения
критерия управления равно: 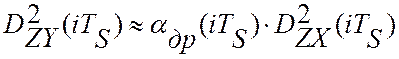 . Как и в случае
робастной стабилизации, оценка скорости дрейфа, Kдр, проводиться по текущим значениям
взаимокорреляционной функции, KYX(iTS) и текущим значениям квадрата отклонения управляющего
воздействия, ∆X2(iTS):
. Как и в случае
робастной стабилизации, оценка скорости дрейфа, Kдр, проводиться по текущим значениям
взаимокорреляционной функции, KYX(iTS) и текущим значениям квадрата отклонения управляющего
воздействия, ∆X2(iTS):
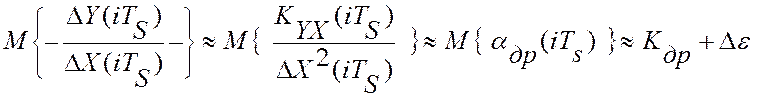
где ![]() - это
погрешность текущей идентификации.
- это
погрешность текущей идентификации.
При этом, потери эффективности, обусловленные остаточным дрейфом можно оценивать по массиву текущих значений критерия управления, ZY(iTS) (см. рис. 3.8):
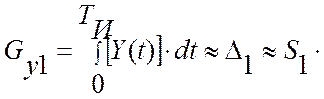
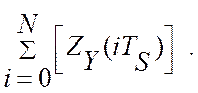 (8.9)
(8.9)
где 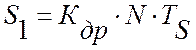 –
адаптивная настройка виртуального прибора, зависящая от настроек модуля вывода
аналоговой информации,
–
адаптивная настройка виртуального прибора, зависящая от настроек модуля вывода
аналоговой информации, 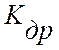 – оценка скорости
дрейфа критерия управления на интервале идентификации;
– оценка скорости
дрейфа критерия управления на интервале идентификации; ![]() –
показания виртуального прибора, регистрирующие текущие значения критерия
управления, Y(t).
–
показания виртуального прибора, регистрирующие текущие значения критерия
управления, Y(t).
Как видно из рис. 3.9, потери остаточного дрейфа при оптимальном управлении состоят из M– периодов идентификации и могут быть вычислены по соотношению:
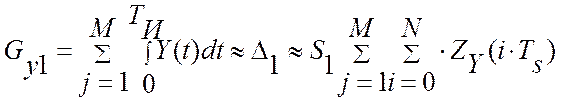 , (8.10)
, (8.10)
где: M– количество интервалов идентификации, по которой
производится оценка потерь; TS - темп сбора текущих значений с датчиков измерительной информации; TИ – период идентификации; N – длина массива показаний
виртуального (программно-аппаратного) прибора, ![]() -
текущее значение критерия управления, Y(t),
-
текущее значение критерия управления, Y(t), 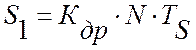 – адаптивная
настройка виртуального прибора.
– адаптивная
настройка виртуального прибора.
8.3.3 Потери эффективности от ошибок идентификации
Третья
составляющая потерь тесно связана с особенностями функционирования алгоритмов текущей идентификации,
описанных в теме 6, и алгоритмов визуализации текущего положения рабочей точки на критерии управления.
Как было показано выше, настроечные коэффициенты, при адаптивном управлении,
зависят от скорости дрейфа критерия управления и должны постоянно
корректироваться в реальном масштабе времени, по текущим значениям
взаимокорреляционной функции, KZX(iTS) и текущим значениям квадрата отклонения управляющего
воздействия, ∆X2(iTS), от предыдущих координат рабочей точки по алгоритму: 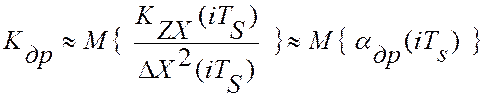 . Эта процедура является одной из самых
распространённых в безмодельных робастных системах [1, 2] и используется не
только для идентификации положения рабочей точки
. Эта процедура является одной из самых
распространённых в безмодельных робастных системах [1, 2] и используется не
только для идентификации положения рабочей точки
![]()
![]()
![]()
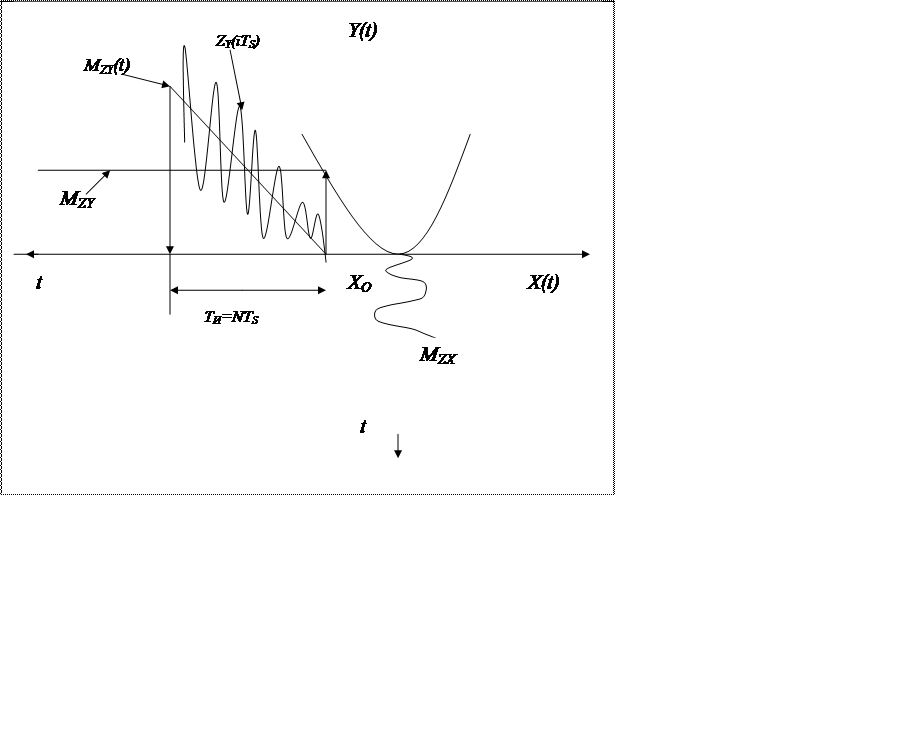
Рис. 8.8 (С. 30) Образование потерь на периоде идентификации
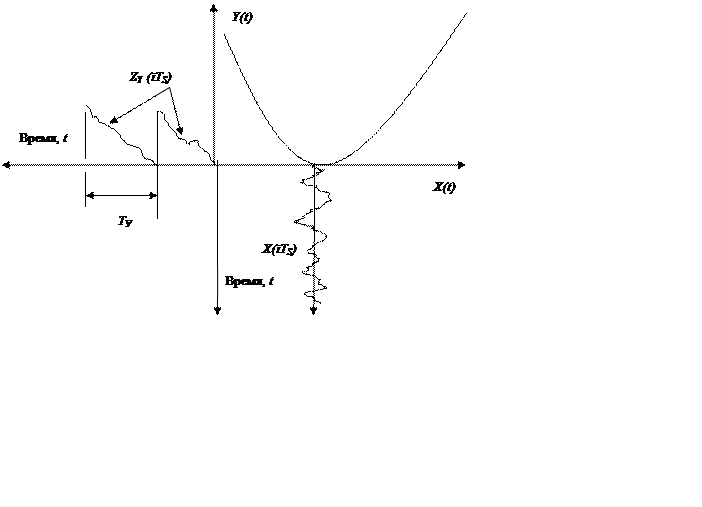
Рис. 8.9 (С. 31) Образование суммарных потерь от остаточного дрейфа
объекта на критерии управления (см. тема 4). Она широко используется и для идентификации свойств объекта (см. тема 5). Эта процедура текущей идентификации (см.тема 6) широко применяется как в робастных системах с упрощенной эталонной моделью, так и в робастных системах с полной эталонной моделью ещё и потому, что эти алгоритмы идентификации позволяют провести анализ погрешностей текущей идентификации и их влияние на потери эффективности.
Пусть текущие значения критерия управления изменяются по закону:
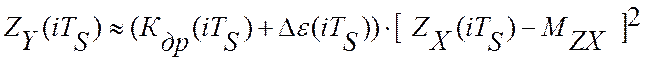 (3.11)
(3.11)
где 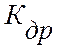 (iTS)- текущее значение скорости дрейфа критерия управления
полученная идентификацией через текущие значения взаимокорреляционной функции;
(iTS)- текущее значение скорости дрейфа критерия управления
полученная идентификацией через текущие значения взаимокорреляционной функции; ![]() (iTS) – текущее значение ошибки идентификации;
(iTS) – текущее значение ошибки идентификации; 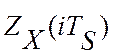 - текущие значения управляющего
воздействия;
- текущие значения управляющего
воздействия; ![]() - оценка математического
ожидания управляющего воздействия на периоде идентификации.
- оценка математического
ожидания управляющего воздействия на периоде идентификации.
Пусть ![]() , тогда текущее значение скорости дрейфа
критерия управления можно оценить производной по времени:
, тогда текущее значение скорости дрейфа
критерия управления можно оценить производной по времени: 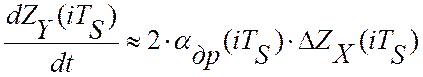 . Выбирая время измерения равное 1 секунде
(
. Выбирая время измерения равное 1 секунде
(![]() ) получаем, что
) получаем, что 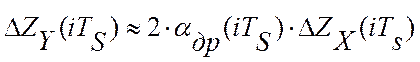 ,
откуда текущее значение скорости дрейфа критерия управления равно:
,
откуда текущее значение скорости дрейфа критерия управления равно: 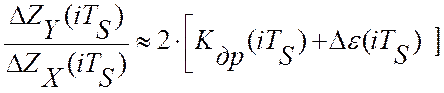 . Откуда текущее значение квадрата
отклонения показаний виртуального прибора будет равно:
. Откуда текущее значение квадрата
отклонения показаний виртуального прибора будет равно:
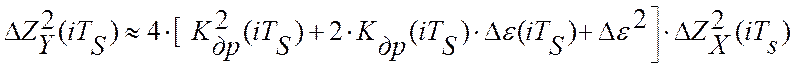 . Для
случая некоррелированности скорости дрейфа и ошибки идентификации это выражение
преобразуется к виду:
. Для
случая некоррелированности скорости дрейфа и ошибки идентификации это выражение
преобразуется к виду:
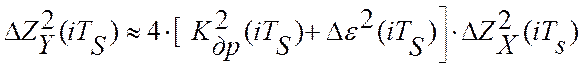 .
.
Откуда следует, что текущее значение квадрата ошибки идентификации равно:
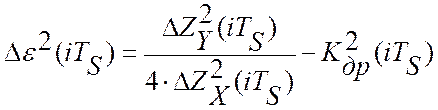
Текущие значения скорости дрейфа
можно определять (см. гл. 2.3) по алгоритму: 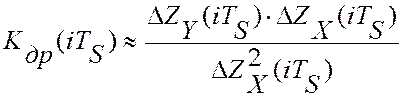 , в
котором числителем является текущее значение взаимокорреляционной функции, а ∆Z2X(iTS) – квадрат отклонения управляющего воздействия от
оценки математического ожидания на интервале идентификации. Учитывая вид
эталонной модели, текущее значение квадрата ошибки можно переписать в виде:
, в
котором числителем является текущее значение взаимокорреляционной функции, а ∆Z2X(iTS) – квадрат отклонения управляющего воздействия от
оценки математического ожидания на интервале идентификации. Учитывая вид
эталонной модели, текущее значение квадрата ошибки можно переписать в виде: 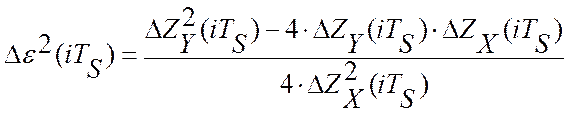 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.